题目内容
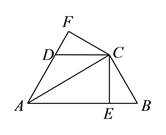
【题目】如图，△ABC中，∠A=40°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF= 度．
【答案】75
【解析】
试题分析：首先根据三角形的内角和定理求得∠ACB的度数，以及∠BCD的度数，根据角平分线的定义求得∠BCE的度数，则∠ECD可以求解，然后在△CDF中，利用内角和定理即可求得∠CDF的度数．
∵∠A=40°，∠B=70°， ∴∠ACB=180°﹣∠A﹣∠B=70°． ∵CE平分∠ACB，
∴∠ACE=
∠ACB=35°． ∵CD⊥AB于D， ∴∠CDA=90°， ∠ACD=180°﹣∠A﹣∠CDA=50°．
∴∠ECD=∠ACD﹣∠ACE=15°． ∵DF⊥CE， ∴∠CFD=90°， ∴∠CDF=180°﹣∠CFD﹣∠DCF=75°．
练习册系列答案
相关题目
