题目内容
【题目】在平面直角坐标系xOy中，已知抛物线y=x2﹣2mx+m2﹣9． 
（1）求证：无论m为何值，该抛物线与x轴总有两个交点；
（2）该抛物线与x轴交于A，B两点，点A在点B的左侧，且OA＜OB，与y轴的交点坐标为（0，﹣5），求此抛物线的解析式；
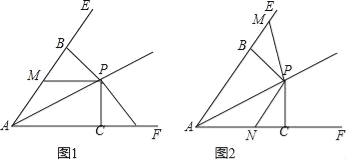
（3）在（2）的条件下，抛物线的对称轴与x轴的交点为N，若点M是线段AN上的任意一点，过点M作直线MC⊥x轴，交抛物线于点C，记点C关于抛物线对称轴的对称点为D，点P是线段MC上一点，且满足MP= 
MC，连结CD，PD，作PE⊥PD交x轴于点E，问是否存在这样的点E，使得PE=PD？若存在，求出点E的坐标；若不存在，请说明理由．
【答案】
（1）证明：令y=0，则x2﹣2mx+m2﹣9=0，
∵△=（﹣2m）2﹣4m2+36＞0，
∴无论m为何值时方程x2﹣2mx+m2﹣9=0总有两个不相等的实数根，
∵抛物线y=x2﹣2mx+m2﹣9的开口向上，顶点在x轴的下方，
∴该抛物线与x轴总有两个交点．
（2）解：∵抛物线y=x2﹣2mx+m2﹣9与y轴交点坐标为（0，﹣5），
∴﹣5=m2﹣9．
解得：m=±2．
当m=﹣2，y=0时，x2+4x﹣5=0
解得：x1=﹣5，x2=1，
∵抛物线y=x2﹣2mx+m2﹣9与x轴交于A，B两点（点A在点B的左侧，且OA＜OB），
∴m=﹣2不符合题意，舍去．
∴m=2．
∴抛物线的解析式为y=x2﹣4x﹣5；
（3）解：如图2，假设E点存在，
∵MC⊥EM，CD⊥MC，
∴∠EMP=∠PCD=90°．
∴∠MEP+∠MPE=90°
∵PE⊥PD，
∴∠EPD=90°，
∴∠MPE+∠DPC=90°
∴∠MEP=∠CPD．
在△EMP和△PCD中，
，
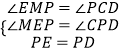∴△EPM≌△PDC（AAS）．
∴PM=DC，EM=PC
设C（x0，y0），则D（4﹣x0，y0），P（x0， 
y0）．
∴2x0﹣4= y0．
∵点C在抛物线y=x2﹣4x﹣5上；
∴y0═x02﹣4x0﹣5
∴2x0﹣4= （x02﹣4x0﹣5）．
解得：x01=1，x02=11（舍去），
∴P（1，﹣2）．
∴PC=6．∴ME=PC=6．
∴E（7，0）．
【解析】（1）令y=0，则x2﹣2mx+m2﹣9=0，根据根的判别式b2﹣4ac=（﹣2m）2﹣4（m2﹣9）=36＞0，所以无论m为何值，该抛物线与x轴总有两个交点．（2）直接将C点（0，﹣5）代入y=x2﹣2mx+m2﹣9根据抛物线与x轴交于A，B两点（点A在点B的左侧，且OA＜OB），求出m的值即可；（3）假设E点存在由直角三角形的性质可以得出∠MEP=∠CPD．再根据条件可以得出△EPM≌△PDC就有PM=DC，EM=PC，设C（x0 ， y0），则D（4﹣x0 ， y0），P（x0 ， y0）．根据PM=DC就有2x0﹣4=﹣ y0 ， 由C点在抛物线上有2x0﹣4=﹣ （ x02﹣4x0﹣5），求出x0的值就可以得出结论．
