Question

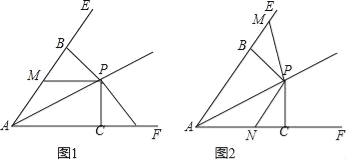
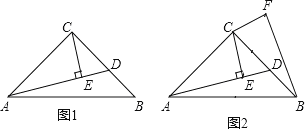
【题目】在等腰Rt△ABC中，∠ACB=90°，AC=BC，点D是边BC上任意一点，连接AD，过点C作CE⊥AD于点E．

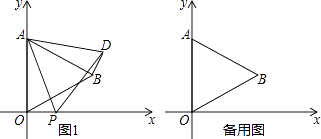
（1）如图1，若∠BAD=15°，且CE=1，求线段BD的长；

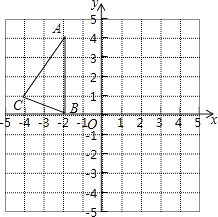
（2）如图2，过点C作CF⊥CE，且CF=CE，连接BF，

求证：AE=BF．

Answer 1

【答案】(1) 2﹣；(2)见解析.

【解析】

解：（1）∵∠ACB=90°，AC=BC，

∴∠CAB=45°，

∵∠BAD=15°，

∴∠CAE=45°﹣15°=30°，

Rt△ACE中，CE=1，

∴AC=2CE=2，

Rt△CED中，∠ECD=90°﹣60°=30°，

∴CD=2ED，

设ED=x，则CD=2x，

∴CE=x，

∴x=1，

x=，

∴CD=2x=，

∴BD=BC﹣CD=AC﹣CD=2﹣；

（2）如图2，

∵∠ACB=∠ECF=90°，

∴∠ACE=∠BCF，

∵AC=BC，CE=CF，

∴△ACE≌△BCF，

∴AE=BF．