题目内容
如图，∠AOB=60°，点M是射线OB上的点，OM=4，以点M为圆心，2cm为半径作圆．若OA绕点O按逆时针方向旋转，当OA和⊙M相切时，OA旋转的角度是______．
如图；
①当OA旋转到OE位置时，与圆M相切于点E，连接ME；
则ME=2，∠MEO=90°；
Rt△OEM中，sin∠MOE=
=
，
∴∠MOE=30°，
∴∠AOE=∠AOB-∠MOE=30°；
②当OA旋转到OF位置时，与圆M相切于点F，连接MF；
则MF=2，∠MFO=90°；
Rt△OFM中，sin∠MOF=
=
，
∴∠MOF=30°，
∴∠AOF=∠AOB+∠FOB=90°；
故OA旋转的角度为30°或90°．
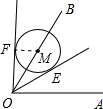
①当OA旋转到OE位置时，与圆M相切于点E，连接ME；
则ME=2，∠MEO=90°；
Rt△OEM中，sin∠MOE=
| ME |
| OM |
| 1 |
| 2 |
∴∠MOE=30°，
∴∠AOE=∠AOB-∠MOE=30°；
②当OA旋转到OF位置时，与圆M相切于点F，连接MF；
则MF=2，∠MFO=90°；
Rt△OFM中，sin∠MOF=
| MF |
| OM |
| 1 |
| 2 |
∴∠MOF=30°，
∴∠AOF=∠AOB+∠FOB=90°；
故OA旋转的角度为30°或90°．
练习册系列答案
相关题目
交于点G，垂足分别是E、F，AC是⊙O的弦，
