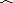题目内容
如图所示，AB是⊙O直径，OD过弦BC的中点F，且交⊙O于点E，若∠AEC=∠ODB．求证：直线BD和⊙O相切．
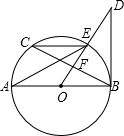
证明：连接AC，
∴∠AEC=∠ABC，
∵∠AEC=∠ODB，
∴∠ODB=∠ABC．
∵O，F分别是AB，BC的中点，
∴AC∥OD，
∴∠BOD=∠BAC．
∵∠BAC+∠ABC=90°，
∴∠ODB+∠BOD=90°．
∴OB⊥BD，即直线BD和⊙O相切．
∴∠AEC=∠ABC，
∵∠AEC=∠ODB，
∴∠ODB=∠ABC．
∵O，F分别是AB，BC的中点，
∴AC∥OD，
∴∠BOD=∠BAC．
∵∠BAC+∠ABC=90°，
∴∠ODB+∠BOD=90°．
∴OB⊥BD，即直线BD和⊙O相切．
练习册系列答案
相关题目
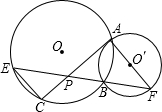与AC相交于点P．
，垂足为F．
