��Ŀ����
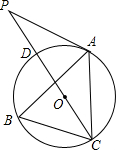
��ͼ����ֱ������ϵxoy�У�O������ԭ�㣬��A��x�������ϣ�OA=12
cm����B��y����������ϣ�OB=12cm������P�ӵ�O��ʼ��OA��2
cm/s���ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��4cm/s���ٶ����B�ƶ�������R�ӵ�B��ʼ��BO��2cm/s���ٶ����O�ƶ������P��Q��R�ֱ��O��A��Bͬʱ�ƶ����ƶ�ʱ��Ϊt��0��t��6��s��
��1�����OAB�Ķ�����
��2����OBΪֱ���ġ�O����AB���ڵ�M����tΪ��ֵʱ��PM���O�����У�
��3��д����PQR�����S�涯���ƶ�ʱ��t�ĺ�����ϵʽ������s����Сֵ����Ӧ��tֵ��
��4���Ƿ���ڡ�APQΪ���������Σ������ڣ������Ӧ��tֵ������������˵�����ɣ�

| 3 |
| 3 |
��1�����OAB�Ķ�����
��2����OBΪֱ���ġ�O����AB���ڵ�M����tΪ��ֵʱ��PM���O�����У�
��3��д����PQR�����S�涯���ƶ�ʱ��t�ĺ�����ϵʽ������s����Сֵ����Ӧ��tֵ��
��4���Ƿ���ڡ�APQΪ���������Σ������ڣ������Ӧ��tֵ������������˵�����ɣ�

��1����Rt��AOB��
tan��OAB=
=
=
��
���OAB=30�㣮
��2����ͼ������O��P��O��M��
��PM���O������ʱ���У�
��PMO��=��POO��=90�㣬
��PMO��ա�POO�䣮
�ɣ�1��֪��OBA=60�㣬
��O��M=O��B��
���O��BM�ǵȱ������Σ�
���BO��M=60�㣮
�ɵá�OO��P=��MO��P=60�㣮
��OP=OO��•tan��OO��P
=6��tan60��=6
��
�֡�OP=2
t��
��2
t=6
��t=3��
����t=3ʱ��PM���O�����У�
��3����ͼ������Q��QE��x�ڵ�E��
�ߡ�BAO=30�㣬AQ=4t��
��QE=
AQ=2t��
AE=AQ•cos��OAB=4t��
=2
t��
��OE=OA-AE=12
-2
t��
��Q���������12
-2
t��2t����
S��PQR=S��OAB-S��OPR-S��APQ-S��BRQ
=
•12•12
-
•2
t•(12-2t)-
(12
-2
t)•2t-
•2t(12
-2
t)
=6
t2-36
t+72
=6
(t-3)2+18
�� ��0��t��6��
��t=3ʱ��S��PQR��С=18
��
��4���������������ͼ
�ٵ�AP=AQ1=4tʱ��
��OP+AP=12
��
��2
t+4t=12
��
��t=
��
��Ϊt=12
-18��
�ڵ�PQ2=AQ2=4tʱ��
��Q2����Q2E��x���ڵ�E��
��PA=2AE=2AQ2•cosA=4
t��
��2
t+4
t=12
��
��t=2��
�۵�PA=PQ3ʱ������P��PH��AB�ڵ�H��
AH=PA•cos30��=��12
-2
t��•
=18-3t��
AQ3=2AH=36-6t��
��36-6t=4t��
��t=3.6��
������������t=2��t=3.6��t=12
-18ʱ����APQ�ǵ��������Σ�
tan��OAB=
| OB |
| OA |
| 12 | ||
12
|
| ||
| 3 |
���OAB=30�㣮
��2����ͼ������O��P��O��M��
��PM���O������ʱ���У�
��PMO��=��POO��=90�㣬
��PMO��ա�POO�䣮
�ɣ�1��֪��OBA=60�㣬
��O��M=O��B��
���O��BM�ǵȱ������Σ�
���BO��M=60�㣮
�ɵá�OO��P=��MO��P=60�㣮
��OP=OO��•tan��OO��P
=6��tan60��=6
| 3 |
�֡�OP=2
| 3 |
��2
| 3 |
| 3 |
����t=3ʱ��PM���O�����У�
��3����ͼ������Q��QE��x�ڵ�E��
�ߡ�BAO=30�㣬AQ=4t��
��QE=
| 1 |
| 2 |
AE=AQ•cos��OAB=4t��
| ||
| 2 |
| 3 |
��OE=OA-AE=12
| 3 |
| 3 |
��Q���������12
| 3 |
| 3 |
S��PQR=S��OAB-S��OPR-S��APQ-S��BRQ
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
=6
| 3 |
| 3 |
| 3 |
=6
| 3 |
| 3 |
��t=3ʱ��S��PQR��С=18
| 3 |
��4���������������ͼ
�ٵ�AP=AQ1=4tʱ��
��OP+AP=12
| 3 |

��2
| 3 |
| 3 |
��t=
6
| ||
|
��Ϊt=12
| 3 |
�ڵ�PQ2=AQ2=4tʱ��
��Q2����Q2E��x���ڵ�E��
��PA=2AE=2AQ2•cosA=4
| 3 |
��2
| 3 |
| 3 |
| 3 |
��t=2��
�۵�PA=PQ3ʱ������P��PH��AB�ڵ�H��
AH=PA•cos30��=��12
| 3 |
| 3 |
| ||
| 2 |
AQ3=2AH=36-6t��
��36-6t=4t��
��t=3.6��
������������t=2��t=3.6��t=12
| 3 |


��ϰ��ϵ�д�
�����Ŀ






 ��AC�ཻ�ڵ�P��
��AC�ཻ�ڵ�P��