题目内容
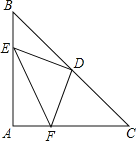
【题目】如图,△ABC是等腰直角三角形, AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.
(1)请说明:DE=DF;
(2)请说明:BE2+CF2=EF2;
(3)若BE=6,CF=8,求△DEF的面积(直接写结果).
【答案】(1)证明见解析;(2)证明见解析;(3)25.
【解析】
(1)连接AD,根据等腰直角三角形性质和直角三角形斜边上中线性质求出∠B=∠C=∠BAD=∠DAC=45°,AD=BD,求出∠BDE=∠ADF,根据ASA证△BDE≌△ADF即可;
(2)根据AAS证△ADE≌△CDF,推出AE=CF,根据勾股定理求出即可;
(3)求出EF长,根据勾股定理求出DE和DF,根据三角形的面积公式求出即可.
(1)证明:连接AD,
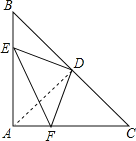
∵等腰直角三角形ABC,
∴∠C=∠B=45°,
∵D为BC的中点,
∴AD⊥BC,AD=BD=DC,AD平分∠BAC,
∴∠DAC=∠BAD=45°=∠B,∠ADC=90°,
∵DE⊥DF,
∴∠EDF=90°,
∴∠ADF+∠FDC=90°,∠FDC+∠BDE=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中
 ,
,
∴△BDE≌△ADF,
∴DE=DF.
(2)证明:∵△BDE≌△ADF,
∴BE=AF,
∵∠EDF=∠ADC=90°,
∴∠EDA+∠ADF=∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△ADE和△CDF中
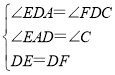 ,
,
∴△ADE≌△CDF,
∴CF=AE,
∴EF2=AE2+AF2=BE2+CF2,
即BE2+CF2=EF2.
(3)解:EF2=BE2+CF2=100,
∴EF=10,
根据勾股定理DE=DF=5![]() ,
,
△DEF的面积是![]() DE×DF=
DE×DF=![]() ×5
×5![]() ×5
×5![]() =25.
=25.
答:△DEF的面积是25.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案【题目】某校举办了一![]() 次趣味数学竞赛,满分
次趣味数学竞赛,满分![]() 分,学生得分均为整数,成绩达到
分,学生得分均为整数,成绩达到![]() 分及以上为合格,达到
分及以上为合格,达到![]() 分及以上为优秀这次竞赛中,甲、乙两组学生成绩如下(单位:分).
分及以上为优秀这次竞赛中,甲、乙两组学生成绩如下(单位:分).
甲组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 90% | 30% |
乙组 | b | c | 196 | 80% | 20% |
以上成绩统计分析表中![]() ________分,
________分,![]() _________分,
_________分,![]() ________分;
________分;
(2)小亮同学说:![]() 这次竞赛我得了
这次竞赛我得了![]() 分,在我们小组中排名属中游略偏上!
分,在我们小组中排名属中游略偏上!![]() 观察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由.
观察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由.
(3)如果你是该校数学竞赛的教练员,现在需要你选择一组同学代表学校参加复赛,你会选择哪一组?并说明理由.