题目内容
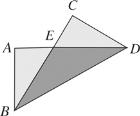
【题目】矩形的周长为24cm,一边中点与对边两顶点连线成直角,则矩形两邻边长分别为___和___.
【答案】4cm 8cm
【解析】
作出图形,根据矩形的对边相等,四个角都是直角,利用“边角边”证明△ABE和△DCE全等,根据全等三角形对应边相等可得BE=CE,从而得到△BCE是等腰直角三角形,然后求出△ABE与△CDE都是等腰直角三角形,从而得到矩形的短边等于长边的一半,然后根据矩形的周长进行计算即可得解.
如图,

∵E是AD的中点,
∴AE=DE,
在△ABE和△DCE中,
 ,
,
∴△ABE≌△DCE(SAS),
∴BE=CE,
∵BE⊥CE,
∴△BCE是等腰直角三角形,
∴∠EBC=∠ECB=45°,
∴∠ABE=∠DCE=90°-45°=45°,
∴△ABE与△CDE都是等腰直角三角形,
∴AB=AE=![]() AD,
AD,
∴2(AB+AD)=2(AD+![]() AD)=3AD=24,
AD)=3AD=24,
解得AD=8cm,
AB=![]() ×8=4cm,
×8=4cm,
即,此矩形的长边和短边长分别是4cm,8cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目