题目内容
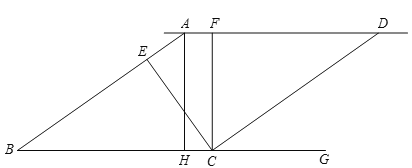
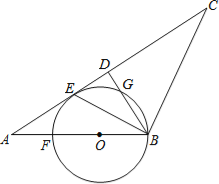
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

【答案】见解析
【解析】试题分析:(1)根据题中条件可证明△AOB≌△AOD,得到OD=OB,可证点D在△ABE的外接圆上;
(2)根据∠C=90°,可得∠CED+∠CDE=90°;利用∠ODE=∠DEC,可知∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°,即CD与△ABE的外接圆相切.
试题解析:证明:(1)∵∠B=90°,∴AE是△ABE外接圆的直径.
取AE的中点O,则O为圆心,连接OB、OD.
在△AOB和△AOD中,∵AB=AD,∠BAC=∠DAO,AO=AO,∴△AOB≌△AOD.∴OD=OB,∴点D在△ABE的外接圆上.
(2)直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90°.∴∠C=90°,∴∠CED+∠CDE=90°.
又∵OE=OD,∴∠ODE=∠OED.
又∠AED=∠CED,∴∠ODE=∠DEC,∴∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°,∴CD与△ABE的外接圆相切.

练习册系列答案
相关题目
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价-进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.