ƒøƒ⁄»ð
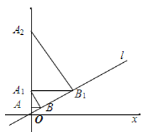
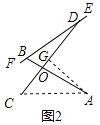
°æƒø°ø»ÁÕº1 «“ªøÓ°∞¿◊¥Ô Ω°±¿¡»À“Œ£Æµ±¿¡»À“ŒÕÍ»´’πø™ ±£¨∆‰≤ý√Ê æ“‚Õº»ÁÕº2À˘ æ£¨Ω Ù∏ÀAB°¢CD‘⁄µ„O¥¶¡¨Ω”£¨«“∑÷±”ÎΩ Ù∏ÀEF‘⁄µ„B£¨D¥¶¡¨Ω”£ÆΩ Ù∏ÀCDµƒOD≤ø∑÷ø…“‘…ÏÀı£®º¥ODµƒ≥§∂»ø…±‰£©£Æ“—÷™OA£Ω50cm£¨OB£Ω20cm£¨OC£Ω30cm£ÆDE£ΩBF£Ω5cm£Æµ±∞—¿¡»À“ŒÕÍ»´µ˛∫œ ±£¨Ω Ù∏ÀAB£¨CD£¨EF÷ÿ∫œ‘⁄“ªÃı÷±œþ…œ£®»ÁÕº3À˘ 棩£¨¥À ±µ„E∫Õµ„A÷ÿ∫œ£Æ
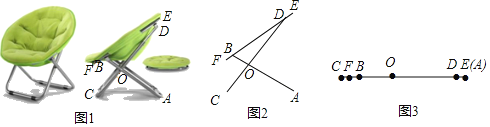
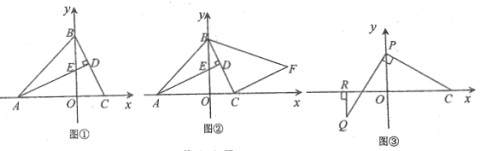
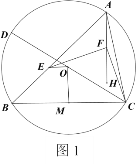
£®1£©»ÁÕº2£¨“—÷™°œBOD£Ω6°œODB£¨°œOBF£Ω140°„£Æ
¢Ÿ«Û°œAOCµƒ∂» ˝£Æ
¢⁄«Ûµ„A£¨C÷ƺ‰µƒæý¿Î£Æ
£®2£©»ÁÕº3£¨µ±¿¡»À“ŒÕÍ»´µ˛∫œ ±£¨«ÛCF”ÎCDµƒ≥§£Æ
°æ¥∞∏°ø£®1£©¢Ÿ120°„£¨¢⁄70cm£ª£®2£©70cm
°æΩ‚Œˆ°ø
£®1£©¢Ÿœ»∏˘æðÕ‚Ω«∂®¿Ìµ√µΩ°œOBF£Ω°œBOD+°œODB£¨∏˘æð“—÷™Ãıº˛πÿ”⁄°œODB∫Õ°œOBFµ»¡øπÿœµ6°œODB+°œODB£Ω°œOBF£¨¥˙»Î ˝÷µº¥ø…«Ûµ√Ω·π˚.
¢⁄◊˜¥πœþ£¨”…£®1£©ø…µ√°œAOC£Ω120°„£¨Ω¯∂¯«Ûµ√°œOAG£Ω90°„©Å60°„£Ω30°„£¨∏˘æð30°„À˘∂‘÷±Ω«±þ «–±±þµƒ“ª∞ε√µΩOG£Ω![]() OA£Ω25£¨∏˘æðπ¥π…∂®¿Ì«Û≥ˆAG°¢CG£¨‘Ÿ∏˘æðAC£Ω
OA£Ω25£¨∏˘æðπ¥π…∂®¿Ì«Û≥ˆAG°¢CG£¨‘Ÿ∏˘æðAC£Ω![]() º¥ø…«Û≥ˆΩ·π˚.
º¥ø…«Û≥ˆΩ·π˚.
£®2£©π€≤ÏÕº–Œø…µ√µΩCF£ΩOC©ÅOB©ÅBF£¨CD£ΩOC+OA©ÅDE£¨¥˙»Î ˝÷µø…µ√Ω·π˚.
Ω‚£∫£®1£©¢Ÿ°þ°œOBF£Ω°œBOD+°œODB£¨°œBOD£Ω6°œODB£¨
°ý6°œODB+°œODB£Ω°œOBF£¨
°ý7°œODB£Ω140°„£¨
°ý°œODB£Ω20°„£¨
°ý°œBOD£Ω6°¡20°„£Ω120°„£¨
°þ°œAOC£Ω°œBOD£¨
°ý°œAOC£Ω120°„£ª
¢⁄¡¨Ω”AC£¨π˝µ„A◊˜AG°ÕCE”⁄G£¨»ÁÕº2À˘ æ£∫
°þ°œAOC£Ω120°„£¨
°ý°œAOG£Ω180°„©Å120°„£Ω60°„£¨
°þAG°ÕCE£¨
°ý°œOGA£Ω90°„£¨
°ý°œOAG£Ω90°„©Å60°„£Ω30°„£¨
°ýOG£Ω![]() OA£Ω
OA£Ω![]() °¡50£Ω25£®cm£©£¨
°¡50£Ω25£®cm£©£¨
”…π¥π…∂®¿Ìµ√£∫AG£Ω![]() £Ω
£Ω![]() £Ω25
£Ω25![]() £®cm£©£¨
£®cm£©£¨
°þCG£ΩOC+OG£Ω30+25£Ω55£®cm£©£¨
°ýAC£Ω![]() £Ω
£Ω![]() £Ω70£®cm£©£¨
£Ω70£®cm£©£¨
°ýµ„A£¨C÷ƺ‰µƒæý¿ÎŒ™70cm£ª
£®2£©CF£ΩOC©ÅOB©ÅBF£Ω30©Å20©Å5£Ω5£®cm£©£¨CD£ΩOC+OA©ÅDE£Ω30+50©Å5£Ω75£®cm£©£Æ

 ”≈“Ì–°∞Ô ÷Õ¨≤Ωø⁄À„œµ¡–¥∞∏
”≈“Ì–°∞Ô ÷Õ¨≤Ωø⁄À„œµ¡–¥∞∏