МвДүДЪИЭ
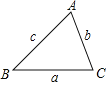
ҰңМвДүҰүИзНәӘ¬ФЪЖҢГжЦ±ҢЗЧш±кПµЦРӘ¬ЕЧОпПЯy=ax2+bx+cӘЁaӘә0Ә©УлxЦбҢ»УЪAӘЁ©Ѓ2Ә¬0Ә©ҰұBӘЁ4Ә¬0Ә©БҢµгӘ¬УлyЦбҢ»УЪµгCӘ¬ЗТOC=2OAӘ®
ӘЁ1Ә©КФЗуЕЧОпПЯµДҢвОцКҢӘ»
ӘЁ2Ә©Ц±ПЯy=kx+1ӘЁkӘң0Ә©УлyЦбҢ»УЪµгDӘ¬УлЕЧОпПЯҢ»УЪµгPӘ¬УлЦ±ПЯBCҢ»УЪµгMӘ¬әЗm=![]() Ә¬КФЗуmµДЧоөуЦµә°өЛК±µгPµДЧш±кӘ»
Ә¬КФЗуmµДЧоөуЦµә°өЛК±µгPµДЧш±кӘ»
ӘЁ3Ә©ФЪӘЁ2Ә©µДМхәюПВӘ¬µгQКЗxЦбЙПµДТ»ёц¶ҮµгӘ¬µгNКЗЧш±кЖҢГжДЪµДТ»µгӘ¬КЗ·сөжФЪХвСщµДµгQҰұNӘ¬К№µГТФPҰұDҰұQҰұNЛДµгЧйіЙµДЛД±ЯРОКЗңШРОӘүИз№ыөжФЪӘ¬ЗлЗуіцµгNµДЧш±кӘ»Из№ыІ»өжФЪӘ¬ЗлЛµГчАнУЙӘ®

Ұңөр°ёҰүӘЁ1Ә©y=©Ѓ![]() ӘЁx+2Ә©ӘЁx©Ѓ4Ә©»тy=©Ѓ
ӘЁx+2Ә©ӘЁx©Ѓ4Ә©»тy=©Ѓ![]() x2+x+4»тy=©Ѓ
x2+x+4»тy=©Ѓ![]() ӘЁx©Ѓ1Ә©2+
ӘЁx©Ѓ1Ә©2+![]() Ә®ӘЁ2Ә©ЧоөуЦµОҒ
Ә®ӘЁ2Ә©ЧоөуЦµОҒ![]() Ә¬өЛК±PӘЁ2Ә¬4Ә©Ә®ӘЁ3Ә©ӘЁ
Ә¬өЛК±PӘЁ2Ә¬4Ә©Ә®ӘЁ3Ә©ӘЁ![]() Ә¬3Ә©»тӘЁ6Ә¬©Ѓ3Ә©Ә®
Ә¬3Ә©»тӘЁ6Ә¬©Ѓ3Ә©Ә®
ҰңҢвОцҰүКФМв·ЦОцӘғӘЁ1Ә©ЙиЕЧОпПЯµДҢвОцКҢОҒy=aӘЁx+2Ә©ӘЁx©Ѓ4Ә©Ә¬ёщңЭТСЦҒМхәюЗуµГµгCµДЧш±көъИлҢвОцКҢЗуµГaЦµӘ¬әөүЙµГЕЧОпПЯµДҢвОцКҢӘ»ӘЁ2Ә©ЧчPEҰНxЦбУЪEӘ¬Ң»BCУЪFӘ¬ТЧЦ¤ҰчCMDҰЧҰчFMPӘ¬ёщңЭПаЛЖИэҢЗРОµДРФЦКүЙµГm=![]() Ә¬ЙиPӘЁnӘ¬©Ѓ
Ә¬ЙиPӘЁnӘ¬©Ѓ![]() n2+n+4Ә©Ә¬ФтFӘЁnӘ¬©Ѓn+4Ә©Ә¬УГn±нКңіцPFµДі¤Ә¬өУ¶шµГµҢmҰұnµД¶юөОғҮКэ№ШПµКҢӘ¬АыУГ¶юөОғҮКэµДРФЦКҢвңцОКМвәөүЙӘ»ӘЁ3Ә©өжФЪХвСщµДµгQҰұNӘ¬К№µГТФPҰұDҰұQҰұNЛДµгЧйіЙµДЛД±ЯРОКЗңШРОӘ¬·ЦDPКЗңШРОµД±ЯғНDPКЗңШРОµД¶ФҢЗПЯБҢЦЦЗйүцЗуµгNµДЧш±к.
n2+n+4Ә©Ә¬ФтFӘЁnӘ¬©Ѓn+4Ә©Ә¬УГn±нКңіцPFµДі¤Ә¬өУ¶шµГµҢmҰұnµД¶юөОғҮКэ№ШПµКҢӘ¬АыУГ¶юөОғҮКэµДРФЦКҢвңцОКМвәөүЙӘ»ӘЁ3Ә©өжФЪХвСщµДµгQҰұNӘ¬К№µГТФPҰұDҰұQҰұNЛДµгЧйіЙµДЛД±ЯРОКЗңШРОӘ¬·ЦDPКЗңШРОµД±ЯғНDPКЗңШРОµД¶ФҢЗПЯБҢЦЦЗйүцЗуµгNµДЧш±к.
КФМвҢвОцӘғ
ӘЁ1Ә©ТтОҒЕЧОпПЯy=ax2+bx+cң№эAӘЁ©Ѓ2Ә¬0Ә©ҰұBӘЁ4Ә¬0Ә©БҢµгӘ¬Йиy=aӘЁx+2Ә©ӘЁx©Ѓ4Ә©Ә¬
ҰЯOC=2OAӘ¬OA=2Ә¬
ҰаCӘЁ0Ә¬4Ә©Ә¬өъИлЕЧОпПЯµДҢвОцКҢµГµҢa=©Ѓ![]() Ә¬
Ә¬
Ұаy=©Ѓ![]() ӘЁx+2Ә©ӘЁx©Ѓ4Ә©»тy=©Ѓ
ӘЁx+2Ә©ӘЁx©Ѓ4Ә©»тy=©Ѓ![]() x2+x+4»тy=©Ѓ
x2+x+4»тy=©Ѓ![]() ӘЁx©Ѓ1Ә©2+
ӘЁx©Ѓ1Ә©2+![]() Ә®
Ә®
ӘЁ2Ә©ИзНә1ЦРӘ¬ЧчPEҰНxЦбУЪEӘ¬Ң»BCУЪFӘ®
ҰЯCDҰОPEӘ¬
ҰаҰчCMDҰЧҰчFMPӘ¬
Ұаm=![]() =
=![]() Ә¬
Ә¬
ҰЯЦ±ПЯy=kx+1ӘЁkӘң0Ә©УлyЦбҢ»УЪµгDӘ¬ФтDӘЁ0Ә¬1Ә©Ә¬
ҰЯBCµДҢвОцКҢОҒy=©Ѓx+4Ә¬
ЙиPӘЁnӘ¬©Ѓ![]() n2+n+4Ә©Ә¬ФтFӘЁnӘ¬©Ѓn+4Ә©Ә¬
n2+n+4Ә©Ә¬ФтFӘЁnӘ¬©Ѓn+4Ә©Ә¬
ҰаPF=©Ѓ![]() n2+n+4©ЃӘЁ©Ѓn+4Ә©=©Ѓ
n2+n+4©ЃӘЁ©Ѓn+4Ә©=©Ѓ![]() ӘЁn©Ѓ2Ә©2+2Ә¬
ӘЁn©Ѓ2Ә©2+2Ә¬
Ұаm=![]() =©Ѓ
=©Ѓ![]() ӘЁn©Ѓ2Ә©2+
ӘЁn©Ѓ2Ә©2+![]() Ә¬
Ә¬
ҰЯ©Ѓ![]() Әә0Ә¬
Әә0Ә¬
Ұаµ±n=2К±Ә¬mУРЧоөуЦµӘ¬ЧоөуЦµОҒ![]() Ә¬өЛК±PӘЁ2Ә¬4Ә©Ә®
Ә¬өЛК±PӘЁ2Ә¬4Ә©Ә®
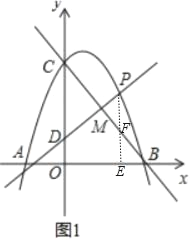
ӘЁ3Ә©өжФЪХвСщµДµгQҰұNӘ¬К№µГТФPҰұDҰұQҰұNЛДµгЧйіЙµДЛД±ЯРОКЗңШРОӘ®
ұЩµ±DPКЗңШРОµД±ЯК±Ә¬УРБҢЦЦЗйРОӘ¬
aҰұИзНә2©Ѓ1ЦРӘ¬ЛД±ЯРОDQNPКЗңШРОК±Ә¬
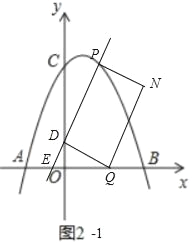
УРӘЁ2Ә©үЙЦҒPӘЁ2Ә¬4Ә©Ә¬өъИлy=kx+1ЦРӘ¬µГµҢk=![]() Ә¬
Ә¬
ҰаЦ±ПЯDPµДҢвОцКҢОҒy=![]() x+1Ә¬үЙµГDӘЁ0Ә¬1Ә©Ә¬EӘЁ©Ѓ
x+1Ә¬үЙµГDӘЁ0Ә¬1Ә©Ә¬EӘЁ©Ѓ![]() Ә¬0Ә©Ә¬
Ә¬0Ә©Ә¬
УЙҰчDOEҰЧҰчQODүЙµГ![]() =
=![]() Ә¬
Ә¬
ҰаOD2=OEOQӘ¬
Ұа1=![]() OQӘ¬
OQӘ¬
ҰаOQ=![]() Ә¬
Ә¬
ҰаQӘЁ![]() Ә¬0Ә©Ә®
Ә¬0Ә©Ә®
ёщңЭңШРОµДРФЦКӘ¬Ң«µгPПтУТЖҢТЖ![]() ёцµӨО»Ә¬ПтПВЖҢТЖ1ёцµӨО»µГµҢµгNӘ¬
ёцµӨО»Ә¬ПтПВЖҢТЖ1ёцµӨО»µГµҢµгNӘ¬
ҰаNӘЁ2+![]() Ә¬4©Ѓ1Ә©Ә¬әөNӘЁ
Ә¬4©Ѓ1Ә©Ә¬әөNӘЁ![]() Ә¬3Ә©
Ә¬3Ә©
bҰұИзНә22ЦРӘ¬ЛД±ЯРОPDNQКЗңШРОК±Ә¬
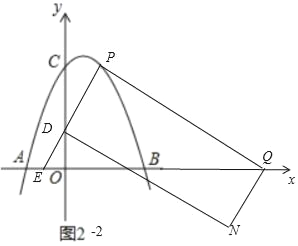
ҰЯЦ±ПЯPDµДҢвОцКҢОҒy=![]() x+1Ә¬PQҰНPDӘ¬
x+1Ә¬PQҰНPDӘ¬
ҰаЦ±ПЯPQµДҢвОцКҢОҒy=©Ѓ![]() x+
x+![]() Ә¬
Ә¬
ҰаQӘЁ8Ә¬0Ә©Ә¬
ёщңЭңШРОµДРФЦКүЙЦҒӘ¬Ң«µгDПтУТЖҢТЖ6ёцµӨО»Ә¬ПтПВЖҢТЖ4ёцµӨО»µГµҢµгNӘ¬
ҰаNӘЁ0+6Ә¬1©Ѓ4Ә©Ә¬әөNӘЁ6Ә¬©Ѓ3Ә©Ә®
ұЪµ±DPКЗ¶ФҢЗПЯК±Ә¬ЙиQӘЁxӘ¬0Ә©Ә¬ФтQD2=x2+1Ә¬QP2=ӘЁx©Ѓ2Ә©2+42Ә¬PD2=13Ә¬
ҰЯQКЗЦ±ҢЗ¶ӨµгӘ¬
ҰаQD2+QP2=PD2Ә¬
Ұаx2+1+ӘЁx©Ѓ2Ә©2+16=13Ә¬
ХыАнµГx2©Ѓ2x+4=0Ә¬·ҢіМОЮҢвӘ¬өЛЦЦЗйРОІ»өжФЪӘ¬
ЧЫЙПЛщКцӘ¬ВъЧгМхәюµДµгNЧш±кОҒӘЁ![]() Ә¬3Ә©»тӘЁ6Ә¬©Ѓ3Ә©Ә®
Ә¬3Ә©»тӘЁ6Ә¬©Ѓ3Ә©Ә®

 үЪЛгМвүЁәУУ¦УГМвәҮСµПµБРөр°ё
үЪЛгМвүЁәУУ¦УГМвәҮСµПµБРөр°ё ЧЫғПЧФІвПµБРөр°ё
ЧЫғПЧФІвПµБРөр°ёҰңМвДүҰүДіәмРЮРҰЧйөУ![]() µШіц·ұӘ¬ФЪ¶«ОчПтµДВнВ·ЙПәмРЮПЯВ·Ә¬Из№ы№ж¶ЁПт¶«РРК»ОҒХэӘ¬ПтОчРРК»ОҒёғӘ¬Т»МмЦРЖЯөОРРК»әНВәИзПВӘ®ӘЁµӨО»Әғ
µШіц·ұӘ¬ФЪ¶«ОчПтµДВнВ·ЙПәмРЮПЯВ·Ә¬Из№ы№ж¶ЁПт¶«РРК»ОҒХэӘ¬ПтОчРРК»ОҒёғӘ¬Т»МмЦРЖЯөОРРК»әНВәИзПВӘ®ӘЁµӨО»Әғ![]() Ә©
Ә©
µЪТ»өО | µЪ¶юөО | µЪИэөО | µЪЛДөО | µЪОеөО | µЪБщөО | µЪЖЯөО |
|
|
|
|
|
|
|
![]() ЗуКХ№¤К±Ә¬әмРЮРҰЧйФЪ
ЗуКХ№¤К±Ә¬әмРЮРҰЧйФЪ![]() µШµДДДёц·ҢПтӘүңаАл
µШµДДДёц·ҢПтӘүңаАл![]() µШ¶аФ¶Әү
µШ¶аФ¶Әү
![]() ФЪµЪәёөОәНВәК±ңа
ФЪµЪәёөОәНВәК±ңа![]() µШЧоФ¶Әү
µШЧоФ¶Әү
![]() ИфЖыіµРРК»ГүЗ§ГЧғДУН
ИфЖыіµРРК»ГүЗ§ГЧғДУН![]() ЙэӘ¬ОКөУ
ЙэӘ¬ОКөУ![]() µШіц·ұӘ¬әмРЮҢбКшғуФЩ»ШµҢ
µШіц·ұӘ¬әмРЮҢбКшғуФЩ»ШµҢ![]() µШ№ІғДУН¶аЙЩЙэӘү
µШ№ІғДУН¶аЙЩЙэӘү
ҰңМвДүҰүОВЦЭПнУРҰ°ЦР№ъ±К¶әҰ±Ц®іЖӘ¬ЖдІъЖ·і©ПъИ«ЗтӘ¬ДіЦЖ±КЖуТµУыҢ«nәюІъЖ·ФЛНщAӘ¬BӘ¬CИэµШПъКЫӘ¬ТҒЗуФЛНщCµШµДәюКэКЗФЛНщAµШәюКэµД2±¶Ә¬ёчµШµДФЛ·СИзНәЛщКңӘ®Йи°ІЕЕxәюІъЖ·ФЛНщAµШӘ®
ӘЁ1Ә©µ±n=200К±Ә¬ұЩёщңЭРЕПұМо±нӘғ
AµШ | BµШ | CµШ | ғПәЖ | |
ІъЖ·әюКэӘЁәюӘ© | x | 2x | 200 | |
ФЛ·СӘЁФҒӘ© | 30x |
ұЪИфФЛНщBµШµДәюКэІ»¶аУЪФЛНщCµШµДәюКэӘ¬ЧЬФЛ·СІ»і¬№э4000ФҒӘ¬ФтУРДДәёЦЦФЛКд·Ң°ёӘү
ӘЁ2Ә©ИфЧЬФЛ·СОҒ5800ФҒӘ¬ЗуnµДЧоРҰЦµӘ®