题目内容
某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案1:从包装盒加工厂直接购买,购买所需的费用y1与包装盒数x满足如图的函数关系。
方案2:租凭机器自己加工,所需费用y2(包括租凭机器的费用和生产包装盒的费用)
与包装盒数 满足如图的函数关系。
满足如图的函数关系。

根据图象回答下列问题:
(1)方案1中每个包装盒的价格是多少元?
(2)方案2中租凭机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1,y2,与x的函数表达式
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由。
方案1:从包装盒加工厂直接购买,购买所需的费用y1与包装盒数x满足如图的函数关系。
方案2:租凭机器自己加工,所需费用y2(包括租凭机器的费用和生产包装盒的费用)
与包装盒数
 满足如图的函数关系。
满足如图的函数关系。
根据图象回答下列问题:
(1)方案1中每个包装盒的价格是多少元?
(2)方案2中租凭机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1,y2,与x的函数表达式
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由。

(1)5;(2)20000,2.5;(3)y1=5x,y2=2.5x+20000;(4)当x=8000时,两种方案同样省钱;当x<8000时,选择方案一;当x>8000时,选择方案二.
试题分析:(1)根据图象1可知100个盒子共花费500元,据此可以求出盒子的单价;
(2)根据图2可以知道租赁机器花费20000元,根据图象所经过的点的坐标求出盒子的单价即可;
(3)根据图象经过的点的坐标用待定系数法求得函数的解析式即可;
(4)求出当x的值为多少时,两种方案同样省钱,并据此分类讨论最省钱的方案即可.
试题解析:(1)500÷100=5,
∴方案一的盒子单价为5元;
(2)根据函数的图象可以知道租赁机器的费用为20000元,
盒子的单价为(30000-20000)÷4000=2.5,
故盒子的单价为2.5元;
(3)设图象一的函数解析式为:y1=k1x,
由图象知函数经过点(100,500),
∴500=100k1,
解得k1=5,
∴函数的解析式为y1=5x;
设图象二的函数关系式为y2=k2x+b
由图象知道函数的图象经过点(0,20000)和(4000,30000)
∴
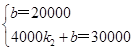 ,
,解得:
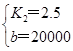
∴函数的解析式为y2=2.5x+20000;
(4)令5x=2.5x+20000,
解得x=8000,
∴当x=8000时,两种方案同样省钱;
当x<8000时,选择方案一;
当x>8000时,选择方案二.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
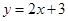 ,求:
,求: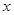 轴,
轴,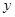 轴的交点坐标;
轴的交点坐标;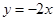
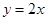
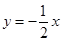
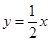
 的解为 .
的解为 .
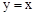 ,
,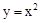 和
和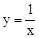 的图象
的图象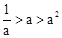 ,那么
,那么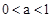 ;
;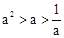 ,那么
,那么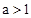 ;
;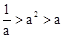 ,那么
,那么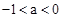 ;
;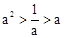 时,那么
时,那么 .
.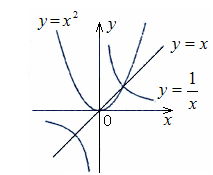
 =
= +
+ 与正比例函数y =
与正比例函数y = (
( 、
、 ≠0)的图象的是( )
≠0)的图象的是( )