题目内容
某租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地收割小麦,其中30台派往A地,20台派往B地.两地区与该租赁公司商定的每天的租赁价格如下:
(1)设派往A地x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),请用x表示y,并注明x的范围.
(2)若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案写出.
| | 甲型收割机的租金 | 乙型收割机的租金 |
| A地 | 1800元/台 | 1600元/台 |
| B地 | 1600元/台 | 1200元/台 |
(2)若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案写出.
(1)y=200x+74000,(10≤x≤30);(2)有三种方案,详见解析.
试题分析:本题考查的是用一次函数解决实际问题,根据题意列出函数式以及根据题意列出不等式结合自变量的取值范围确定方案.(1)派往A地x台乙型联合收割机,那么派往B地(30-x)台,派往A地的(30-x)台甲型收割机,派往B地(20-30+x)台,可得y=(30-x)×1800+(x-10)×1600+1600x+(30-x)×1200,10≤x≤30.
(2)根据题意可列不等式(30-x)×1800+(x-10)×1600+1600x+(30-x)×1200≥79600,解出x后根据自变量的取值范围来确定有几种方案.
试题解析:
解:(1)y=(30-x)×1800+(x-10)×1600+1600x+(30-x)×1200=200x+74000,
10≤x≤30;
(2)200x+74000≥79600,
解得x≥28,
三种方案,依次为x=28,29,30的情况
①当x=28时,派往A地28台乙型联合收割机,那么派往B地2台乙,派往A地的2台甲型收割机,派往B地18台甲.
②当x=29时,派往A地29台乙型联合收割机,那么派往B地1台乙,派往A地的1台甲型收割机,派往B地19台甲.
③当x=30时,派往A地30台乙型联合收割机,那么派往B地0台乙,派往A地的0台甲型收割机,派往B地20台甲.

练习册系列答案
相关题目
 (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
 (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式; 满足如图的函数关系。
满足如图的函数关系。

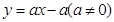 的大致图象是( )
的大致图象是( )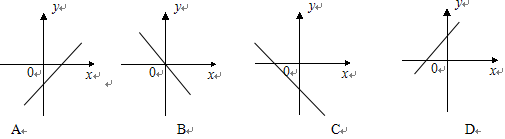
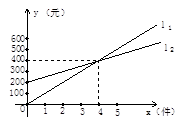
 和
和 的图像交于点P(-2,-5),则根据图像可得不等式
的图像交于点P(-2,-5),则根据图像可得不等式 的解集是 .
的解集是 .
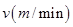 和时间
和时间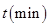 的函数关系的是( )
的函数关系的是( )