Question

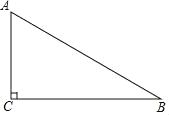
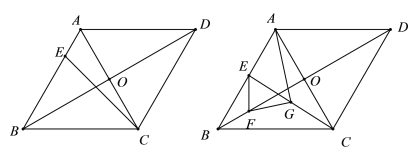
【题目】如图，已知在中，，在上取点，使得，若．

（1）求证：；

（2）若平分，求的度数．

Answer 1

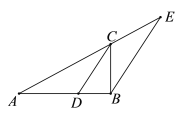
【答案】（1）见解析；（2）∠ABE＝120°．

【解析】

（1）欲证明AB=BE，只需推知∠A=∠E即可．
（2）由三角形内角和定理和等腰三角形的性质求得∠A=30°，结合（1）中的∠A=∠E和△ABE的内角和是180°解答．

（1）∵AD＝CD ∴∠A＝∠ACD．

又∵CD∥BE ∴∠ACD＝∠E．

∴∠A＝∠E．

∴AB＝BE；

（2）∵在Rt△ABC中，∠ABC＝90°

∴∠A+∠ACB＝90°．

∵CD平分∠ACB，

∴∠ACD＝∠BCD．

又∵∠A＝∠ACD，

∴∠A+∠ACD+∠BCD＝3∠A＝90°．

∴∠A＝30°．

∵由（1）得∠A＝∠E＝30°．

∴∠ABE＝180°﹣2∠A＝120°．