题目内容
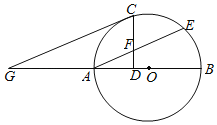
【题目】如图,在菱形ABCD中,AC,BD相交于点O,BC=2OC,E为AB边上一点.
(1)若CE=6,∠ACE=15°,求BC的长;
(2)若F为BO上一点,且BF=EF,G为CE中点,连接FG,AG,求证:![]()
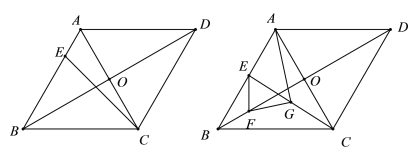
【答案】(1)BC=![]() +
+![]() ;(2)见解析;
;(2)见解析;
【解析】
(1)过点E作EM⊥BC于点M,由菱形的性质和已知条件可得AB=BC=AC,进一步利用锐角三角函数解RT△CEM和RT△BEM,求出BM和CM的值,相加即可得到BC的长;
(2)延长FG至点H,使GH=FG,连接CH,AH.先证△EFG≌△CHG得到CH=BF,CH∥EF,再延长EF交BC于点K,证△AFB≌△AHC,进一步证得∠AFH=60°,最后由三角函数可得出![]() .
.
(1)过点E作EM⊥BC于点M,

∵四边形ABCD是菱形,AC与BD交于点O
∴AB=BC,AC=2CO
∵BC=2CO
∴AB=BC=AC
∴∠ACB=∠ABC=60°
∵∠ACE=15°
∴∠ECB=∠ACB—∠ACE=45°
∴CM=EM=![]() CE=
CE=![]()
∴BM=![]() EM=
EM=![]()
∴BC= CM+BM=![]() +
+![]()
(2)证明:延长FG至点H,使GH=FG,连接CH,AH.
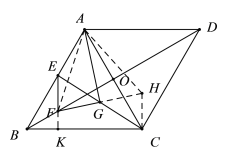
∵G为CE中点,∴EG=GC,
在△EFG与△CHG中,
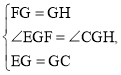 ,
,
△EFG≌△CHG(SAS),
∴EF=CH,∠CHG=∠EFG,
∴CH=BF,CH∥EF,
延长EF交BC于点K

∵菱形ABCD中,BD平分∠ABC∴∠ABF=![]() ∠ABC=30°
∠ABC=30°
∵BF=EF ∴∠BEF=∠ABF =30°
又∵∠ABC=60°∴∠EKB=90°
∵CH//EF ∴∠HCB=∠EKB=90°
∴∠ACH=∠HCB—∠ACB=90°﹣60°=30°,
∴∠ABF=∠ACH
∵BF=EF,EF=CH
∴BF=CH
在△AFB与△AHC中,

△AFB≌△AHC(SAS),
∴AF=AH,∠BAF=∠CAH
∵FG=GH,
∴AG⊥FG
∵∠BAC=∠BAF+∠FAC=60°,
∴∠CAH+∠FAC=60°,
即∠FAH=60°,
∴∠AFH=60°
∴AG=![]() FG
FG