题目内容
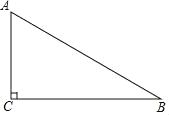
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连接AP,若AP平分∠CAB,求∠B的度数.
【答案】(1)作图见解析;(2)30°.
【解析】
(1)作线段AB的垂直平分线即可;
(2)根据线段垂直平分线的性质可得BP=AP,根据等边对等角可得∠B=∠PAB,然后再根据角平分线定义可得∠CAP=∠PAB,进而可得∠B=∠PAB=∠CAP,然后可得答案
解:(1)如图:作线段AB的垂直平分线;
(2)∵PD是线段AB的垂直平分线,
∴PA=PB,
∴∠B=∠PAB,
∵AP平分∠CAB,
∴∠CAP=∠PAB,
∴∠B=∠PAB=∠CAP,
∵∠ACB=90°,
∴∠B=∠PAB+∠CAP=90°,
∴∠B=30°.

练习册系列答案
相关题目