题目内容
如图,抛物线y=-x2+5x+m经过点A(1,0),与y轴交于点B,
(1)求m的值;
(2)若抛物线与x轴的另一交点为C,求△CAB的面积;
(3)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
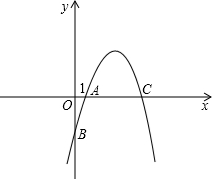
(1)求m的值;
(2)若抛物线与x轴的另一交点为C,求△CAB的面积;
(3)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.

(1)根据题意,把点A的坐标代入抛物线方程得:
0=-1+5+m,即得m=-4;
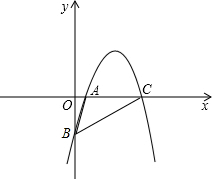 (2)根据题意得:
(2)根据题意得:
令y=0,即-x2+5x-4=0,解得x1=1,x2=4,
∴点C坐标为(4,0);
令x=0,解得y=-4,
∴点B的坐标为(0,-4);
∴由图象可得,△CAB的面积S=
×OB×AC=
×4×3=6;
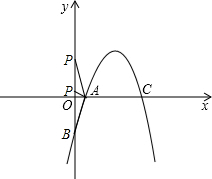 (3)根据题意得:
(3)根据题意得:
①当点O为PB的中点,设点P的坐标为(0,y),(y>0)
则y-4=0,即得y=4,
∴点P的坐标为(0,4).
②当AB=BP时,AB=
,
∴OP的长为:
-4,
∴P(0,
-4),
∴P(0,
-4),或(0,4)
0=-1+5+m,即得m=-4;
 (2)根据题意得:
(2)根据题意得:令y=0,即-x2+5x-4=0,解得x1=1,x2=4,
∴点C坐标为(4,0);
令x=0,解得y=-4,
∴点B的坐标为(0,-4);
∴由图象可得,△CAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
 (3)根据题意得:
(3)根据题意得:①当点O为PB的中点,设点P的坐标为(0,y),(y>0)
则y-4=0,即得y=4,
∴点P的坐标为(0,4).
②当AB=BP时,AB=
| 17 |
∴OP的长为:
| 17 |
∴P(0,
| 17 |
∴P(0,
| 17 |

练习册系列答案
相关题目





 点C(如图),点C的坐标为(0,-3),且BO=CO
点C(如图),点C的坐标为(0,-3),且BO=CO 日销售量Q(件)与时间t(天)之间的函数关系是Q=-t+40(0<t≤30,t是整数).
日销售量Q(件)与时间t(天)之间的函数关系是Q=-t+40(0<t≤30,t是整数).