Question

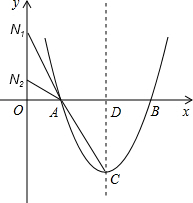
如图，已知抛物线y=ax²+bx+c与x轴交于A（1，0），B（3，0）两点，且过点（-1，16），抛物线的顶点是点C，对称轴与x轴的交点为点D，原点为点O．在y轴的正半轴上有一动点N，使以A、O、N这三点为顶点的三角形与以C、A、D这三点为顶点的三角形相似．求：
（1）这条抛物线的解析式；
（2）点N的坐标．

Answer 1

（1）∵抛物线y=ax²+bx+c经过点A（1，0），B（3，0），（-1，16），
∴

a+b+c=0 9a+3b+c=0 a-b+c=16

，
解得

a=2 b=-8 c=6

，
∴抛物线的解析式为y=2x²-8x+6；

（2）∵y=2x²-8x+6=2（x-2）²-2，
∴顶点C的坐标为（2，-2），
点D的坐标为（2，0），
∴CD=2，
∵A（1，0），
∴AD=2-1=1，
①ON和DC是对应边时，△AON∽△ADC，
∴

ON

DC

=

AO

AD

，
即

ON

2

=

1

1

，
解得ON=2，
∴点N（0，2）；
②ON和DA是对应边时，△AON∽△CDA，
∴

ON

DA

=

AO

CD

，
即

ON

1

=

1

2

，
解得ON=

1

2

，
∴点N（0，

1

2

），
综上所述，点N的坐标为（0，2）或（0，

1

2

）．