题目内容
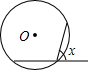
已知圆O的半径为6cm,弦AB=6cm,则弦AB所对的圆周角是______度.
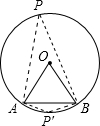
连OA,OB,如图,
∵OA=OB=6cm,AB=6cm,
∴△OAB为等边三角形,
∴∠AOB=60°,
当弦AB所对的圆周角的顶点在优弧AB上,则∠P=
∠AOB=
×60°=30°;
当弦AB所对的圆周角的顶点在劣弧AB上,则∠P′=180°-∠P=180°-30°=150°.
故答案为30°或150°.
∵OA=OB=6cm,AB=6cm,
∴△OAB为等边三角形,
∴∠AOB=60°,
当弦AB所对的圆周角的顶点在优弧AB上,则∠P=
| 1 |
| 2 |
| 1 |
| 2 |
当弦AB所对的圆周角的顶点在劣弧AB上,则∠P′=180°-∠P=180°-30°=150°.
故答案为30°或150°.


练习册系列答案
相关题目