题目内容
如图，在平面直角坐标系中，P是经过O（0，0）、A（0，2）、B（2，0）的圆上一个动点（P与O、B不重合），则∠AOB=______度，∠OPB=______度．
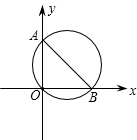
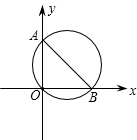
由题意知∠AOB=90°，OA=OB=2；
∴△AOB是等腰直角三角形，∠OAB=45°；
∴∠OCB=∠OAB=45°；
①当P点在优弧OAB上时，∠OPB=∠OAB=45°；
②当P点在劣弧OB上时，∠OPB=180°-∠OAB=135°；
因此∠AOB=90°，∠OPB=45°或135°．
∴△AOB是等腰直角三角形，∠OAB=45°；
∴∠OCB=∠OAB=45°；
①当P点在优弧OAB上时，∠OPB=∠OAB=45°；
②当P点在劣弧OB上时，∠OPB=180°-∠OAB=135°；
因此∠AOB=90°，∠OPB=45°或135°．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
