Question

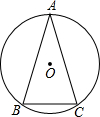
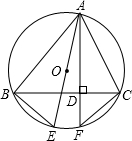
如图，四边形ABCD内接于以AC为直径的⊙O，AC，BD交于点E，DB平分∠ADC，AF∥BD交CD延长线于点F，且CD，DF的长是关于x的方程x²-3x+p=0的两根．
（1）求证：DE=

2

2

p；
（2）求DB的长．

Answer 1

（1）证明：∵AC为直径，
∴∠ADC=90°．
又∵DB平分∠ADC，AF∥BD，
∴∠DAF=∠F=45°．
∴△ADF为等腰直角三角形．
∴AF=

2

DF，AD=DF．
∵CD，DF的长是关于x的方程x²-3x+p=0的两根，
∴CD+DF=CF=3，DF²-3DF+p=0，p=3DF-DF²
∵AF∥BD，
∴△CDE∽△CFA．
∴

DE

AF

=

CD

CD+DF

．
即

DE

2 DF

=

3-DF

3

DE=

2

3

（3DF-DF²）=

2

3

p．

（2）∵∠ABD、∠ACD都是弧AD所对的圆周角，
∴∠ABD=∠ACD．
又∠ADB=∠F=45°，
∴△ABD∽△ACF．
∴

AB

AC

=

BD

CF

．
即

2

2

=

BD

3

．
BD=

3 2

2

．