题目内容
【题目】如图1,![]() 和
和![]() 是两块可以完全重合的三角板,
是两块可以完全重合的三角板,![]() ,
,![]() . 在图1所示的状态下,
. 在图1所示的状态下,![]() 固定不动,将
固定不动,将![]() 沿直线
沿直线![]() 向左平移.
向左平移.
(1)当![]() 移到图2位置时连接位綱连接
移到图2位置时连接位綱连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(2)如图3,在上述平移过程中,当点![]() 与
与![]() 的中点重合时,直线
的中点重合时,直线![]() 与AD有什么位置关系,请写出证明过程.
与AD有什么位置关系,请写出证明过程.

【答案】(1)证明见解析;(2)直线![]() 垂直平分
垂直平分![]() ,证明见解析.
,证明见解析.
【解析】
(1)先找出相等条件,利用三角形全等的判定定理得出三角形全等,从而对应边相等得出结论.
(2)根据边角关系得出三角形DFC是等边三角形,等边三角形的性质证出结论.
(1)证明:∵△ABC和△DEF是两块可以完全重合的三角板,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)连接![]() ,
,
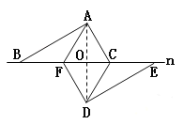
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形
是等腰三角形![]() 的角平分线,
的角平分线,
即![]() 也是等腰三角形
也是等腰三角形![]() 的底边
的底边![]() 上的高和中线,
上的高和中线,
因此直线![]() 垂直平分
垂直平分![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目




