题目内容
【题目】如图,已知等边三角形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别为各边中点,
分别为各边中点,![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 为等边三角形(点
为等边三角形(点![]() 的位置改变时,
的位置改变时,![]() 也随之整体移动).
也随之整体移动).

(1)如图1,当点![]() 在点
在点![]() 左侧时,请判断
左侧时,请判断![]() 与
与![]() 有怎样的数量关系?请直接写出结论,不必证明或说明理由;
有怎样的数量关系?请直接写出结论,不必证明或说明理由;
(2)如图2,当点![]() 在
在![]() 上时,其它条件不变,(1)的结论中
上时,其它条件不变,(1)的结论中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)若点![]() 在点
在点![]() 右侧时,请你在图3中画出相应的图形,并判断(1)的结论中
右侧时,请你在图3中画出相应的图形,并判断(1)的结论中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.(提示:连接
的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.(提示:连接![]() 、
、![]() 、
、![]() .可证
.可证![]() 、
、![]() 、
、![]() 、
、![]() 均为等边三角形).
均为等边三角形).
【答案】(1)![]() ,(2)成立证明见解析;(3)结论仍成立.
,(2)成立证明见解析;(3)结论仍成立.
【解析】
(1)连接DE,DF,得出△DFE是等边三角形,那么∠DEF=∠DFM=60°,DE=DF,再利用SAS证明△MDF和△EDN全等,由此可得出EN=MF.
(2)(3)证法同(1)都要证明△MDF和△EDN全等,证明过程中都要作出三角形的三条中位线,然后根据三条中位线分成的小等边三角形的边和角相等来得出两三角形全等的条件,因此结论仍然成立.
解:(1)EN=MF.理由如下:连接DE,DF,
∵△ABC是等边三角形,∴AB=AC=BC.
又∵D,E,F是三边的中点,∴EF=DF=BF.
∴∠DEF=∠DFM=60°,
又△MDN为等边三角形,∴∠MDN=60°,
∠MDN+∠NDF=∠FDE+∠NDF,
∴∠MDF=∠NDE,
在△EDN和△MDF中,

∴△EDN≌△MDF(SAS),
∴EN=MF.
(2)如图②,EN=MF仍然成立.证明如下:连接DF,NF, 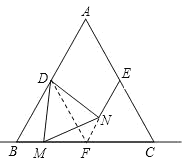
∵△ABC是等边三角形,∴AB=AC=BC.
又∵D,E,F是三边的中点,∴EF=DF=BF.
∵∠BDM+∠MDF=60°,∠FDN+∠MDF=60°,
∴∠BDM=∠FDN,
在△DBM和△DFN中,

∴△DBM≌△DFN,
∴BM=FN,∠DFN=∠FDB=60°,
∴NF∥BD,
∵E,F分别为边AC,BC的中点,
∴EF是△ABC的中位线,
∴EF∥BD,
∴F在直线NE上,
∵BF=EF,
∴MF=EN.
(3)如图③,MF=NE的结论仍然成立.
连接DF、DE,
由(2)知DE=DF,∠NDE=∠FDM,DN=DM,
在△DNE和△DMF中,

∴△DNE≌△DMF,
∴MF=NE.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案【题目】汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x(元) | 3000 | 3200 | 3500 | 4000 |
y(辆) | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数(辆) | ________ | 未租出的车辆数(辆) | ________ |
租出每辆车的月收益(元) | ________ | 所有未租出的车辆每月的维护费(元) | ________ |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.