Question

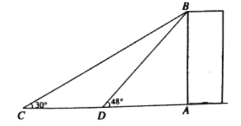
【题目】如图，某校数学兴趣小组要测量大楼AB的高度，他们在点C处测得楼顶B的仰角为30°，再往大楼AB方向前进至点D处测得楼顶B的仰角为48°，CD＝96m，其中点A、D、C在同一直线上．求AD的长和大楼AB的高度（结果精确到1m）参考数据：sin48°≈0．74，cos48°≈0．67，tan48°≈1．11，≈1．73

Answer 1

【答案】AD的长约为105m，大楼AB的高约为116m

【解析】

首先设大楼AB的高度为xm，在Rt△ABC中利用正切函数的定义可求得 ，然后根据∠ADB的正切表示出AD的长，又由CD=96m，可得方程 ，解此方程即可求得答案．

解：设大楼AB的高度为xm，
在Rt△ABC中，∵∠C=30°，∠BAC=90°，
∴ ，
在Rt△ABD中， ，
∴，
∵CD=AC-AD，CD=96m，
∴ ，
解得：x≈116，

∴
答：大楼AB的高度约为116m，AD的长约为105m．