题目内容
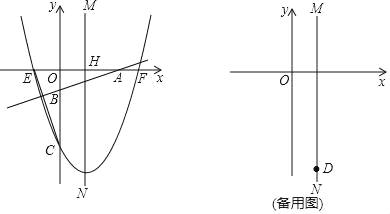
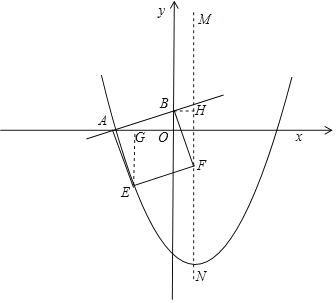
【题目】如图,直角坐标系中,抛物线y=a(x﹣4)2﹣16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y=![]() x+b分别交x,y轴于点A,B.
x+b分别交x,y轴于点A,B.
(1)写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).
(2)若AF=AH=OH,求证:∠CEO=∠ABO.
(3)当b>﹣4时,以AB为边作正方形,使正方形的另外两个顶点一个落在抛物线上,一个落在抛物线的对称轴上,求所有满足条件的a及相应b的值.(直接写出答案即可)
【答案】(1)D(4,﹣16),点C的纵坐标为16a﹣16;(2)见解析;(3)a=![]() ,b=﹣2或a=
,b=﹣2或a=![]() ,b=﹣1或a=
,b=﹣1或a=![]() ,b=4.
,b=4.
【解析】
(1)从抛物线的顶点式就可以知道抛物线的顶点坐标,点C的纵坐标令x=0即可.
(2)求证两个角相等,可以证这两个角的三角函数相等.
(3)分情况讨论,利用全等三角形找到线段之间的数量关系,表示点坐标,代入解析式即可求出a、b.
(1)∵抛物线的解析式为y=a(x﹣4)2﹣16,
∴抛物线的顶点D的坐标为(4,﹣16),
当x=0时,y=16a﹣16,
∴点C的纵坐标为16a﹣16.
(2)∵D(4,﹣16),
∴OH=4.
∵AF=AH=OH,EH=HF,
∴F(12,0),A(8,0),E(﹣4,0),
将点F代入抛物线解析式得:
∴0=a(12﹣4)2﹣16,a![]() ,
,
将点A代入直线解析式得:![]() 8+b=0,b
8+b=0,b![]() ,
,
将a代入点C的纵坐标得:∴16a﹣16=﹣12,
∴C(0,﹣12),OC=12,tan∠CEO![]() 3,tan∠OBA
3,tan∠OBA![]() 3,
3,
∴∠CEO=∠ABO.
(3)分三种情况讨论:
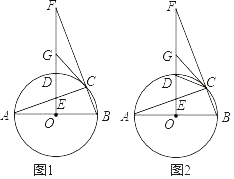
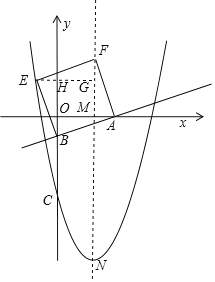
①如图所示.
∵y![]() x+b,当x=0时,y=b,
x+b,当x=0时,y=b,
∴B(0,b),
过点E作EG垂直于NF,设对称轴与x轴的交点为M,BG与y轴的交点为点H.
∵四边形EFAB为正方形,可知△EFG≌△ABO(AAS),△FMA≌△ABO(AAS),∴OB=AM=FG=﹣b.
∵抛物线的对称轴为直线x=4,
∴OA=FM=EG=4﹣b,
∴A(4﹣b,0),E(b,4),
将点A代入直线解析式得:0![]() (4﹣b)+b,解得:b=﹣2,
(4﹣b)+b,解得:b=﹣2,
∴E(﹣2,4),
∴4=a(﹣2﹣4)2﹣16,
解得:a![]() .故a
.故a![]() ,b=﹣2.
,b=﹣2.
②如图所示.
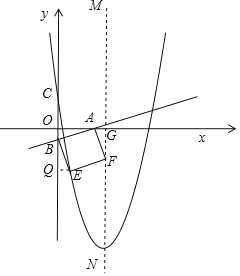
△OBA≌△AFG(AAS),△OBA≌△BEQ(AAS),
∴OB=EQ=AG=﹣b,
∴OA=FG=BQ=4+b,
∴A(4+b,0),E(﹣b,﹣4),
将点A代入直线解析式得:0![]() (4+b)+b,解得:b=﹣1,
(4+b)+b,解得:b=﹣1,
∴E(1,﹣4),将点E(1,﹣4)代入抛物线解析式得:﹣4=a(1﹣4)2﹣16,
解得:a![]() .故a
.故a![]() ,b=﹣1.
,b=﹣1.
③如图所示.
△ABO≌△EAG(AAS),△ABO≌△FBH(AAS),
∴OB=BH=AG=4,
∴b=4,
∴OA=12,EG=12,
∴E(﹣8,﹣12),
代入抛物线解析式得:﹣12=a(﹣8﹣4)2﹣16,解得:a![]() .
.
故a![]() ,b=4.
,b=4.
综上所述:a![]() ,b=﹣2或a
,b=﹣2或a![]() ,b=﹣1或a
,b=﹣1或a![]() ,b=4.
,b=4.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】调查作业:了解你所住小区家庭3月份用气量情况
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
(1)小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.
(2)在表3中,调查的15个家庭中使用气量的中位数是 m3,众数是 m3.
(3)小东将表2中的数据按用气量x(m3)大小分为三类.
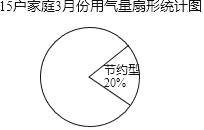
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)小芸算出表3中3月份平均每人的用气量为6m3,请估计该小区3月份的总用气量.