题目内容
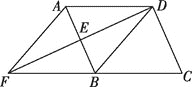
【题目】已知抛物线L:y=ax2+bx+3与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求抛物线的函数表达式及顶点D的坐标;
(2)若将抛物线L沿y轴平移后得到抛物线L′,抛物线L′经过点E(4,1),与y轴的交点为C′,顶点为D′,在抛物线L′上是否存在点M,使得△MCC′的面积是△MDD′面积的2倍?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)C(0,3),D(2,-1);(2)M(4,1)或(![]() ,-
,-![]() ).
).
【解析】
(1)将点A(1,0),B(3,0)代入y=ax2+bx+3,即可确定函数解析式,进而求D坐标;
(2)设平移后解析式y=(x-2)2-1+h,将点E代入可求解析式y=(x-2)2-3,设M(x,x2-4x+1),由面积关系可得|x|=2|x-2|,求得M(4,1)或M(![]() ,-
,-![]() ).
).
(1)将点A(1,0),B(3,0)代入y=ax2+bx+3,
解得a=1,b=-4,
∴y=x2-4x+3,
∴C(0,3),D(2,-1);
(2)设平移后解析式y=(x-2)2-1+h,
∵经过点E(4,1),
∴h=-2,
∴y=(x-2)2-3,
∴C'(0,1),D'(2,-3)
∴CC'=2,DD'=2,
∵△MCC′的面积是△MDD′面积的2倍,
设M(x,x2-4x+1),
∴|x|=2|x-2|,
∴x=4或x=![]() ,
,
∴M(4,1)或(![]() ,-
,-![]() ).
).

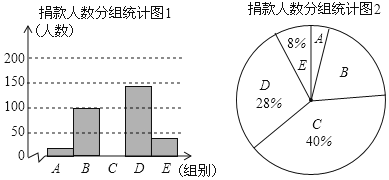
【题目】我校“点爱”社团倡导全校学生参加“关注特殊儿童”自愿捐款活动,并对此次活动进行抽样调查,得到一组学生捐款情况的数据,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.请结合以上信息解答下列问题.
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
(1)a= ,本次抽样调查样本的容量是 ;
(2)补全“捐款人数分组统计图1”;
(3)若记A组捐款的平均数为5元,B组捐款的平均数为15元,C组捐款的平均数为25元,D组捐款的平均数为35元,E组捐款的平均数为50元,全校共有2000名学生参加此次活动,请你估计此次活动可以筹得善款的金额大约为多少元.
【题目】调查作业:了解你所住小区家庭3月份用气量情况
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
(1)小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.
(2)在表3中,调查的15个家庭中使用气量的中位数是 m3,众数是 m3.
(3)小东将表2中的数据按用气量x(m3)大小分为三类.
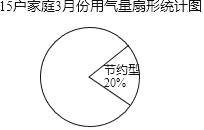
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)小芸算出表3中3月份平均每人的用气量为6m3,请估计该小区3月份的总用气量.