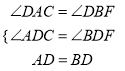Question

【题目】如图，在矩形ABCD中，AB＝1，对角线AC、BD相交于点O，过点O作EF⊥AC分别交射线AD与射线CB于点E和点F，联结CE、AF．

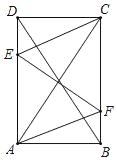
（1）求证：四边形AFCE是菱形；

（2）当点E、F分别在边AD和BC上时，如果设AD＝x，菱形AFCE的面积是y，求y关于x的函数关系式，并写出x的取值范围；

（3）如果△ODE是等腰三角形，求AD的长度．

Answer 1

【答案】（1）见解析；（2）；（3）AD的值为或.

【解析】

（1）由△DOE≌△BOF，推出EO=OF，∵OB=OD，推出四边形EBFD是平行四边形，再证明EB=ED即可．

（2）由cos∠DAC=，求出AE即可解决问题；

（3）分两种情形分别讨论求解即可.

（1）①证明：如图1中，

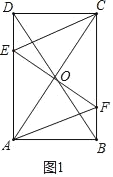
∵四边形ABCD是矩形，

∴AD∥BC，OB＝OD，

∴∠EDO＝∠FBO，

在△DOE和△BOF中，

，

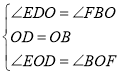∴△DOE≌△BOF，

∴EO＝OF，∵OB＝OD，

∴四边形EBFD是平行四边形，

∵EF⊥BD，OB＝OD，

∴EB＝ED，

∴四边形EBFD是菱形．

（2）由题意可知：，，

∵，

∴，

∴，

∵AE≤AD，

∴，

∴x2≥1，

∵x＞0，

∴x≥1．

即（x≥1）．

（3）①如图2中，当点E在线段AD上时，ED＝EO，则Rt△CED≌Rt△CEO，

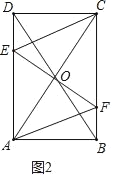
∴CD＝CO＝AO＝1，

在Rt△ADC中，AD＝．

如图3中，当的E在线段AD的延长线上时，DE＝DO，

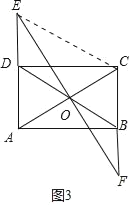
∵DE＝DO＝OC，EC＝CE，

∴Rt△ECD≌Rt△CEO，

∴CD＝EO，

∵∠DAC＝∠EAO，∠ADC＝∠AOE＝90°，

∴△ADC≌△AOE，

∴AE＝AC，

∵EO垂直平分线段AC，

∴EA＝EC，

∴EA＝EC＝AC，

∴△ACE是等边三角形，

∴AD＝CDtan30°＝，

综上所述，满足条件的AD的值为或．