题目内容
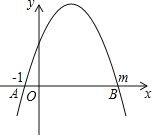
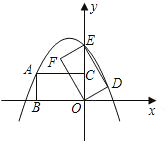
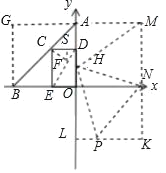
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A在y轴的正半轴上,点B在x轴的负半轴上,点C是线段AB上一动点CD⊥y轴于点D,CE⊥x轴于点E,OA=6,AD=OE.
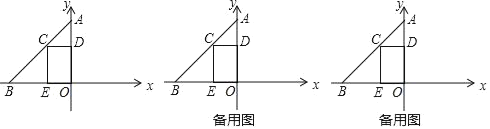
(1)求直线AB的解析式;
(2)连接ED,过点C作CF⊥ED,垂足为F,过点B作x轴的垂线交FC的延长线于点G,求点G的坐标;
(3)在(2)的条件下,连接AG,作四边形AOBG关于y轴的对称图形四边形AONM,连接DN,将线段DN绕点N逆时针旋转90°得到线段PN,H为OD中点,连接MH、PH,四边形MHPN的面积为40,连接FH,求线段FH的长.
【答案】(1)y=x+6;(2)G点坐标为(﹣6,6);(3)![]()
【解析】
(1)易证四边形DCEO为矩形,结合AD=OE,可得AD=CD,△ACD,△ABO是等腰直角三角形,OB=OA=6,从而获得A、B两点的坐标,然后用待定系数法就可以求出AB的解析式;
(2)可使用设参法,设D点坐标为(0,a),用(1)中的几何关系将OD、CE、AD、CD、EO表示出来,继而表示C、E点的坐标,用待定系数法求出直线DE的解析式,根据DE和FG的垂直关系以及C点的坐标求出直线FG的解析式,从而求出点G的坐标;
(3)设AD=a,通过已知的面积关系建立方程,求出a的值,从而获得各点的坐标,在△ADF中利用等面积法求出点F的坐标,从而求出FH的长.
解:(1)∵CD⊥y轴,CE⊥x轴
∴∠CDO=∠CEO=90°
又∵∠DOE=90°
∴四边形DCEO是矩形
∴CD=OE
又∵AD=OE
∴AD=CE
∴AD=CD
∴△ACD是等腰直角三角形
∴∠ACD=45°
∴∠ABO=45°
∴∠ACD=∠ABO
∴AO=BO=6
∴A(0,6),B(﹣6,0)
设直线AB的解析式为y=kx+6
将A(﹣6,0)代入,得0=﹣6k+6
解得,k=1
∴直线AB的解析式为:y=x+6
(2)
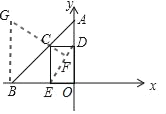
如图所示,设D(0,a),则OD=CE=a,AD=CD=EO=6﹣a
∴C(a﹣6,a),E(a﹣6,0)
设yDE=k1x+a,将E(a﹣6,0)代入,得,
0=(a﹣6)k1+a
解得,![]()
∴yDE=![]()
设yFG=k2x+b1
∵DE⊥FG
∴k1k2=﹣1
∴![]()
∴yFG=![]()
将C(a﹣6,a)代入,得,![]()
解得,![]()
∴yFG=![]() +
+![]()
∵当x=﹣6时,yFG=6
∴G点坐标为(﹣6,6)
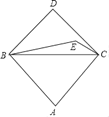
(3)根据题意,如图所示
可证△ODN≌△NPK
∴ON=NK=6
∴四边形ONKL为正方形
设AD=a,则OH=DH=3﹣![]()
PK=OD=6﹣a
LP=a
SMHPN=SAMKL﹣S△AMH﹣S△NKP﹣S△OLP
=6×12﹣![]()
=45﹣3a+![]()
45﹣3a+![]() =40
=40
解得a1=2,a2=10(舍)
作FS⊥CD
可得CD=2,EC=4
∴ED=2![]()
由等面积法
CDCE=EDCF
2×4=2![]() ×CF
×CF
∴CF=![]()
∵CD=2
∴DF=![]()
CDFS=CFFD
FS=![]()
∴SD=![]()
∴F(![]() ,
,![]() )
)
∴![]()

【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.