题目内容
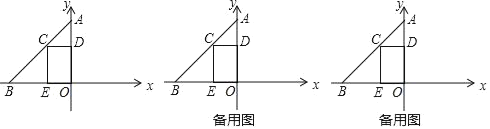
【题目】如图，在平面直角坐标系xOy中，已知抛物线y=ax2-2x+c与直线y=kx+b都经过A（0，-3）、B（3，0）两点，该抛物线的顶点为C．
（1）求此抛物线和直线AB的解析式；
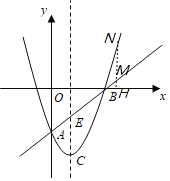
（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；
（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．
【答案】(1) 抛物线的解析式为y=x2-2x-3，直线AB的解析式为y=x-3；(2) M点的坐标为（2，-1）或（
，
）；(3) 当m=
时，△PAB面积的最大值是
，此时P点坐标为（，）．
【解析】
（1）将A（0，-3）、B（3，0）两点坐标分别代入二次函数的解析式和一次函数解析式即可求解；
（2）先求出C点坐标和E点坐标，则CE=2，分两种情况讨论：①若点M在x轴下方，四边形CEMN为平行四边形，则CE=MN，②若点M在x轴上方，四边形CENM为平行四边形，则CE=MN，设M（a，a-3），则N（a，a2-2a-3），可分别得到方程求出点M的坐标；
（3）如图，作PG∥y轴交直线AB于点G，设P（m，m2-2m-3），则G（m，m-3），可由S△PAB＝
PGOB，得到m的表达式，利用二次函数求最值问题配方即可．
（1）∵抛物线y=ax2-2x+c经过A（0，-3）、B（3，0）两点，
∴
，
∴
，
∴抛物线的解析式为y=x2-2x-3，
∵直线y=kx+b经过A（0，-3）、B（3，0）两点，
∴
，解得：
，
∴直线AB的解析式为y=x-3，
（2）∵y=x2-2x-3=（x-1）2-4，
∴抛物线的顶点C的坐标为（1，-4），
∵CE∥y轴，
∴E（1，-2），
∴CE=2，
①如图，若点M在x轴下方，四边形CEMN为平行四边形，则CE=MN，
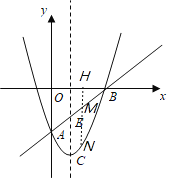
设M（a，a-3），则N（a，a2-2a-3），
∴MN=a-3-（a2-2a-3）=-a2+3a，
∴-a2+3a=2，
解得：a=2，a=1（舍去），
∴M（2，-1），
②如图，若点M在x轴上方，四边形CENM为平行四边形，则CE=MN，
设M（a，a-3），则N（a，a2-2a-3），
∴MN=a2-2a-3-（a-3）=a2-3a，
∴a2-3a=2，
解得：a=，a=
（舍去），
∴M（，），
综合可得M点的坐标为（2，-1）或（，）．
（3）如图，作PG∥y轴交直线AB于点G，
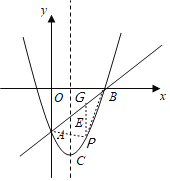
设P（m，m2-2m-3），则G（m，m-3），
∴PG=m-3-（m2-2m-3）=-m2+3m，
∴S△PAB=S△PGA+S△PGB=PGOB＝×(m2+3m)×3=m2+
m=- (m)2+，
∴当m=时，△PAB面积的最大值是，此时P点坐标为（，）．
