题目内容
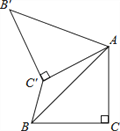
【题目】如图,已知正方形![]() 的边长是
的边长是![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() 于点
于点![]() ,
,![]() 是
是![]() 延长线上一点,且始终保持
延长线上一点,且始终保持![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时:
时:
①求![]() 的值;②若
的值;②若![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
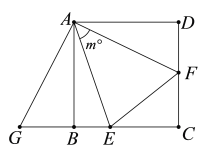
【答案】(1)详见解析;(2)详见解析;(3)①45;②![]()
【解析】
(1)在正方形ABCD中,AB=AD,![]() =90°.已知BG=DF,所以得出△ABG≌△ADF,
=90°.已知BG=DF,所以得出△ABG≌△ADF,
(2)由△ABG≌△ADF,得出∠GAB=∠FAD,从而得到∠GAF=∠GAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,得出结论AG⊥AF;
(3)①由△ABG≌△ADF,AG=AF,BG=DF.得到EF=BE+DF,证出△AEG≌△AEF.所以∠EAG=∠EAF,∠EAF=![]() ∠GAF=45°,即m=45;
∠GAF=45°,即m=45;
②若F是CD的中点,则DF=CF=BG=1.设BE=x,则CE=2-x,EF=EG=1+x.在Rt△CEF中,利用勾股定理得出BE的长为![]() .
.
解:(1)证明:如图:
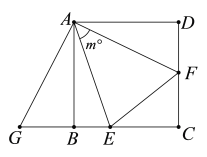
∵在正方形ABCD中,
∴AB=AD,![]() =90°.
=90°.
在![]() 中,
中,
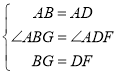
![]() ·
·
(2)证明:
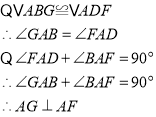
(3)①解:△ABG≌△ADF,
∴AG=AF,BG=DF.
∵EF=BE+DF,
∴EF=BE+BG=EG.
∵AE=AE,
在△AEG和△AEF中.
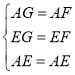
∴△AEG≌△AEF(SSS).
∴∠EAG=∠EAF,
∴∠EAF=![]() ∠GAF=45°,
∠GAF=45°,
即m=45;
②若F是CD的中点,则DF=CF=BG=1.
设BE=x,则CE=2-x,EF=EG=1+x.
在Rt△CEF中,CE2+CF2=EF2,即(2-x)2+12=(1+x)2,得x=![]()
∴BE的长为![]()

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某县某中学开展“庆五四”歌咏比赛活动,八年级(1)、(2)班各选出5名选手参加比赛,两个班选出的5名选手的比赛成绩(满分为100分)如图所示.

(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
八(1) | ________________ | 85 |
八(2) | 80 | ________________ |
(2)请你计算八(1)和八(2)班的平均成绩各是多少分.
(3)结合两班比赛成绩的平均数和中位数,分析哪个班级的比赛成绩较好.
(4)请计算八(1)、八(2)班的比赛成绩的方差,并说明哪个班的成绩比较稳定.