题目内容
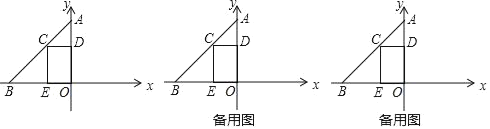
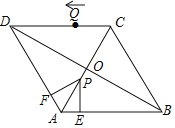
【题目】如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=![]() ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
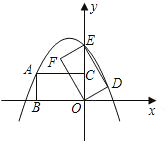
(1)判断点E是否在y轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
【答案】(1)在;(2)![]() ;(3)当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-
;(3)当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-![]() ,2),Q2(
,2),Q2(![]() ,2);当点P2的坐标为(-
,2);当点P2的坐标为(-![]() ,2)时,点Q的坐标分别为Q3(-
,2)时,点Q的坐标分别为Q3(-![]() ,2),Q4(
,2),Q4(![]() ,2).
,2).
【解析】
(1)可连接OA,通过证∠AOE=60°,即与旋转角相同来得出OE在y轴上的结论.
(2)已知了AB,OB的长即可求出A的坐标,在直角三角形OEF中,可用勾股定理求出OE的长,也就能求得E点的坐标,要想得出抛物线的解析式还少D点的坐标,可过D作x轴的垂线,通过构建直角三角形,根据OD的长和∠DOx的正弦和余弦值来求出D的坐标.
求出A、E、D三点坐标后即可用待定系数法求出抛物线的解析式.
(3)可先求出矩形的面积,进而可得出平行四边形OBPQ的面积.由于平行四边形中OB边的长是定值,因此可根据平行四边形的面积求出P点的纵坐标(由于P点在x轴上方,因此P的纵坐标为正数),然后将P点的纵坐标代入抛物线中可求出P点的坐标.求出P点的坐标后,将P点分别向左、向右平移OB个单位即可得出Q点的坐标,由此可得出符合条件的两个P点坐标和四个Q点坐标.
(1)点E在y轴上
理由如下:
连接AO,如图所示,在Rt△ABO中,∵AB=1,BO=![]() ,
,
∴AO=2∴sin∠AOB=![]() ,∴∠AOB=30°
,∴∠AOB=30°
由题意可知:∠AOE=60°∴∠BOE=∠AOB+∠AOE=30°+60°=90°
∵点B在x轴上,∴点E在y轴上.
(2)过点D作DM⊥x轴于点M,

∵OD=1,∠DOM=30°
∴在Rt△DOM中,DM=![]() ,OM=
,OM=![]()
∵点D在第一象限,
∴点D的坐标为(![]() ,
,![]() )
)
由(1)知EO=AO=2,点E在y轴的正半轴上
∴点E的坐标为(0,2)
∴点A的坐标为(-![]() ,1)
,1)
∵抛物线y=ax2+bx+c经过点E,
∴c=2
由题意,将A(-![]() ,1),D(
,1),D(![]() ,
,![]() )代入y=ax2+bx+2中,
)代入y=ax2+bx+2中,
得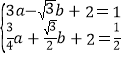
解得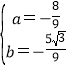
∴所求抛物线表达式为:y=-![]() x2-
x2-![]() x+2
x+2
(3)存在符合条件的点P,点Q.
理由如下:∵矩形ABOC的面积=ABBO=![]()
∴以O,B,P,Q为顶点的平行四边形面积为2![]() .
.
由题意可知OB为此平行四边形一边,
又∵OB=![]()
∴OB边上的高为2
依题意设点P的坐标为(m,2)
∵点P在抛物线y=-![]() x2-
x2-![]() x+2上
x+2上
∴-![]() m2-
m2-![]() m+2=2
m+2=2
解得,m1=0,m2=-![]()
∴P1(0,2),P2(-![]() ,2)
,2)
∵以O,B,P,Q为顶点的四边形是平行四边形,
∴PQ∥OB,PQ=OB=![]() ,
,
∴当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-![]() ,2),Q2(
,2),Q2(![]() ,2);
,2);
当点P2的坐标为(-![]() ,2)时,点Q的坐标分别为Q3(-
,2)时,点Q的坐标分别为Q3(-![]() ,2),Q4(
,2),Q4(![]() ,2).
,2).

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案