题目内容
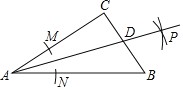
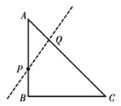
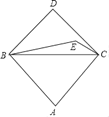
【题目】如图,在△ABC中,AB=AC,以BC为斜边作等腰直角三角形BCD,E是△BCD内一点,连接BE和EC,BE=AB,∠BEC+![]() ∠BAC=180°.若EC=1,tan∠ABC=
∠BAC=180°.若EC=1,tan∠ABC=![]() ,则线段BD的长是_____.
,则线段BD的长是_____.
【答案】![]()
【解析】
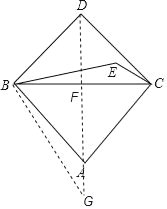
连接AD,并延长DA到G,使得AG=EG=1,连接BG,证明△ABG≌△EBC(SAS),得BG=BC,再设BF=![]() x,在Rt△BGF中,用勾股定理列出x的方程,求得x便可求得BD.
x,在Rt△BGF中,用勾股定理列出x的方程,求得x便可求得BD.
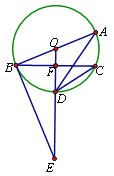
解:连接AD,并延长DA到G,使得AG=EG=1,连接BG,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AD⊥BC,BF=CF,∠BAF=![]() ∠BAC,
∠BAC,
∵∠BEC+![]() ∠BAC=180°,∠BAD+∠BAG=180°,
∠BAC=180°,∠BAD+∠BAG=180°,
∴∠BAG=∠BEC,
∵BA=AE,
∴△ABG≌△EBC(SAS),
∴BG=BC,
∵tan∠ABC=![]() ,
,
∴设BF=![]() x,则AF=2x,BG=BC=2
x,则AF=2x,BG=BC=2![]() x,
x,
∵BG2=BF2+FG2,
∴![]()
解得,x=1,或x=﹣0.2(舍去),
∴BF=![]() ,
,
∴BD=![]() BF=
BF=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目