题目内容
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
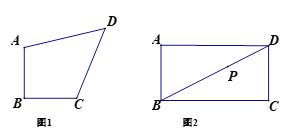
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,则对角线BD的长为 ;
②若AC⊥BD,求证:AD=CD;
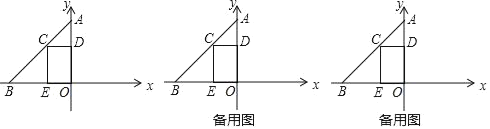
(2)如图2,在矩形ABCD中,AB=5,BC=9,点![]() 是对角线
是对角线![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作直线分别交边
作直线分别交边![]() 于点
于点![]() ,使四边形
,使四边形![]() 是等腰直角四边形.直接写出
是等腰直角四边形.直接写出![]() 的长为 .
的长为 .
【答案】(1)①![]() ;②见解析;(2)5或6.5.
;②见解析;(2)5或6.5.
【解析】
(1)①根据有一组对边平行且相等的四边形是平行四边形可证得四边形ABCD是平行四边形;根据邻边相等的平行四边形是菱形可证得四边形ABCD是菱形;根据有一个角是直角的菱形是正方形可证得四边形ABCD是正方形,从而求出对角边即可.
②根据全等三角形的判定定理可得出三角形全等,然后得出对应边相等即可.
(2)紧抓等腰直角四边形的概念,分类讨论,先根据图形定义可直接得出AE的长度,再结合相似三角形的性质和判定定理可求出AE的长度.
解:(1)①∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
又AB=BC,∠ABC=90°,
∴四边形ABCD是正方形,
∴BD=AC=![]() =
=![]()
所以答案为![]() .
.
②如图1,连接AC,BD,
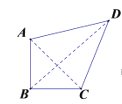
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD,
又∵BD=BD,
∴△ABD≌△CBD,
∴AD=CD.
(2)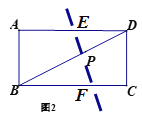
因为四边形ABFE是等腰直角四边形,
所以可以是AB=AE或AB=BF.
当AB=AE时,AE=AB=5,
当AB=BF时,BF=5
∵DE∥BF,
∴△DPE∽△BPF,
∴![]() ,
,
∴DE=2.5
∴AE=9-2.5=6.5
综上,AE结果为5或6.5.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目