题目内容
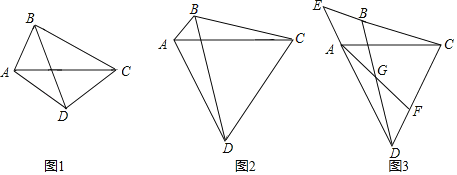
【题目】已知,如图,在△ABC中,AC的垂直平分线与∠ABC的角平分线交于点D,
(1)如图1,判断∠BAD和∠BCD之间的数量关系,并说明理由;
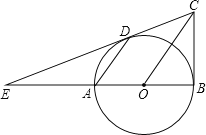
(2)如图2,若∠DAC=60°时,探究线段AB,BC,BD之间的数量关系,并说明理由;
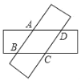
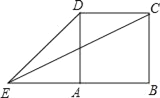
(3)如图3,在(2)的条件下,DA和CB的延长线交于点E,点F是CD上一点且DF=AE,连接AF交BD于点G,若CE=9,求DG的长.
【答案】(1)∠BAD+∠BCD=180°,见解析;(2)BD=AB+BC,见解析;(3)![]() .
.
【解析】
(1)过点D作DG⊥BC于点G,DH⊥BA于点H,根据HL可证明△ADH≌△CDG,可得∠HAD=∠DCG,得出∠BAD+∠BCD=180°;
(2)在BD上截取BF=AB,证明△ABF为等边三角形,△ADC为等边三角形,再证明△ABC≌△AFD,可得出DF=BC,则BD=BF+DF=AB+BC.
(3)延长FD至点M,使DM=DF,证明△EAC≌△MDA,可得AM=CE,∠MAD=∠ECA,可由DG=![]() 得出结果.
得出结果.
(1)∠BAD+∠BCD=180°,理由如下:
如图1,过点D作DG⊥BC于点G,DH⊥BA于点H,
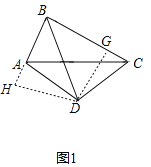
∵AC的垂直平分线与∠ABC角平分线的交于点D,
∴AD=DC,∠ABD=∠DBC,
∴DH=DG,
∴Rt△ADH≌Rt△CDG(HL),
∴∠HAD=∠DCG,
∵∠BAD+∠HAD=180°,
∴∠BAD+∠DCG=180°,
即∠BAD+∠BCD=180°;
(2)BD=AB+BC,理由如下:
如图2,在BD上截取BF=AB,连结AF,
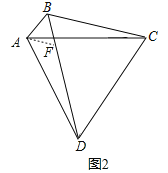
由(1)知∠BAD+∠BCD=180°,
∴∠ABC+∠DAC=180°,
∵∠DAC=60°,
∴∠ABC=120°,
∴∠ABD=∠DBC=60°,
∴△ABF为等边三角形,
∴AB=AF=BF,∠BAF=60°,
∵AD=DC,
∴△ADC为等边三角形,
∴AD=AC,∠DAC=60°,
∴∠DAF=∠BAC,
∴△ABC≌△AFD(SAS),
∴DF=BC,
∴BD=BF+DF=AB+BC.
(3)由(2)知∠DAC=∠DBC=60°,如图3,延长FD至点M,使DM=DF,
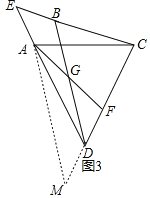
∴∠ACB=∠ADB,
∵DM=DF,DF=AE,
∴DM=AE,
∵∠DAC=∠ADC=60°,
∴∠ADM=∠EAC=120°,
∵AC=AD,
∴△EAC≌△MDA(SAS),
∴AM=CE,∠MAD=∠ECA,
∴∠MAD=∠ADB,
∴DG∥AM,
∵DF=DM,
∴AG=GF,
∴![]() .
.