题目内容
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
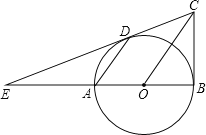
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
【答案】(1)见解析(2)2:3
【解析】解:(1)证明:连接DO,
∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD。
又∵OA=OD,∴∠DAO=∠ADO。
∴∠COD=∠COB。
在△COD和△COB中,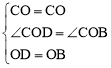 ,
,
∴△COD≌△COB(SAS)。
∴∠CDO=∠CBO=90°.
又∵点D在⊙O上,∴CD是⊙O的切线.

(2)∵△COD≌△COB.∴CD=CB。
∵DE=2BC,∴ED=2CD。
∵AD∥OC,∴△EDA∽△ECO。
∴AD:OC=DE:CE=2:3。
(1)连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线。
(2)由△COD≌△COB.可得CD=CB,即可得DE=2CD,易证得△EDA∽△ECO,然后由相似三角形的对应边成比例,求得AD:OC的值。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目