题目内容
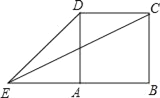
【题目】如图，正方形ABCD的边长为1，延长BA至E，使AE＝1，连接EC、ED，则sin∠CED＝（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
连接AC，作EF⊥CA，交CA的延长线于点F，求出DE∥AC，推出∠CED＝∠ECA，求出EC、EF的长，根据锐角三角函数的定义求出即可．
连接AC，作EF⊥CA，交CA的延长线于点F．
∵四边形ABCD是正方形，∴∠BAC＝45°，∠DAE＝∠DAB＝90°．
∵AD＝AE＝1，∴∠AED＝∠ADE＝45°，即∠DEA＝∠CAB＝45°，∴AC∥ED，∴∠CED＝∠ECA．
∵AE＝1，∴由勾股定理得：EF＝AF
．
∵在Rt△EBC中，由勾股定理得：CE2＝12+22＝5，∴CE
，∴sin∠CED＝sin∠ECF
．
故选B．
练习册系列答案
相关题目
