题目内容
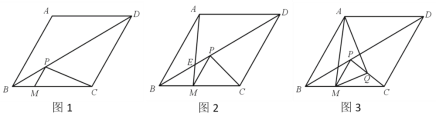
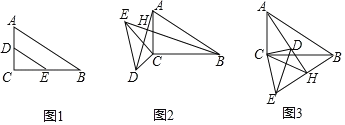
【题目】如图1,ABCD是平行四边形对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F.
(1)求证:AE=CF.
(2)如图2,若ABCD是老张家的一块平行四边形田地。P为水井,现要把这块田地平均分给两个儿子,为了用水方便,要求分给两个儿子的田地都与水井P相邻。请你帮老张家设计一下,画出图形,并说明理由?

【答案】(1)见解析;(2)图和理由见解析
【解析】
(1)利用ASA可证△AOE≌△COF,从而得出AE=CF;
(2)图形设计如下,根据平行四边形的特点,过对角线的交点O的直线可以将平行四边形分为2块面积相等部分,故只需要直线过点O和点P即可.
证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC,OA=OC,
∴![]() DAC=
DAC=![]() BCA
BCA
在△AOE和△COF
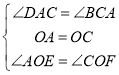
∴△AOE≌△COF(ASA),
∴AE=CF
(2)设计图形如下
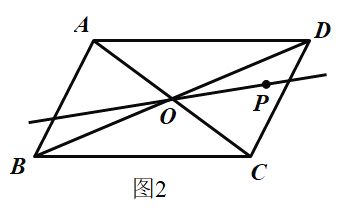
理由:平行四边形是中心对称图形,对称中心是两条对角线的交点,只要满足两块地面积相等,且都与水井相邻就可以。那么可以考虑平行四边形的性质(平行四边形的对角线互相平分)来解题,找到对角线的交点与水井点P的连线的所在直线即可.

练习册系列答案
相关题目