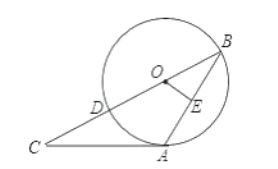
题目内容
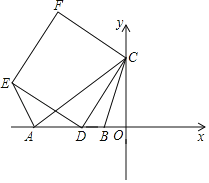
【题目】如图,点O是矩形ABCD的对角线的交点,AB=15,BC=8,直线EF经过点O,分别与边CD,AB相交于点E,F(其中0<DE<![]() ).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
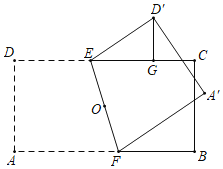
【答案】![]()
![]()
【解析】
如图,连接AC,BD.由题意OD=OC=OD′=![]() ,推出点D′的运动轨迹是弧CD,当OD′⊥CD时,D′G的值最大,设DE=ED′=x,在Rt△EGD′中,根据EG2+D′G2=ED′2,构建方程求出x即可解决问题.
,推出点D′的运动轨迹是弧CD,当OD′⊥CD时,D′G的值最大,设DE=ED′=x,在Rt△EGD′中,根据EG2+D′G2=ED′2,构建方程求出x即可解决问题.
如图,连接AC,BD.
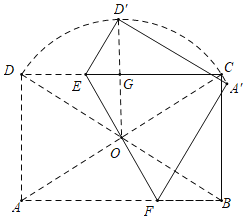
∵四边形ABCD是矩形,
∴AC=BD,∠DAB=90°,AD=BC=8,
∴BD=![]() =17,
=17,
∵OD=OC=OD′=![]() ,
,
∴点D′的运动轨迹是弧CD,
当OD′⊥CD时,D′G的值最大,
∵OG∥BC,OD=OB,
∴DG=GC,
∴OG=![]() BC=4,
BC=4,
∴D′G的最大值=OD′﹣OG=![]() ﹣4=
﹣4=![]() ,
,
设DE=ED′=x,
在Rt△EGD′中,∵EG2+D′G2=ED′2,
∴(![]() ﹣x)2+(
﹣x)2+(![]() )2=x2,
)2=x2,
解得x=![]() ,
,
∴EG=DG﹣DE=![]()
∴OE=![]() =
=![]() ,
,
∴EF=2OE=![]() .
.
故答案为:![]() ,
,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目