ЬтФПФкШн
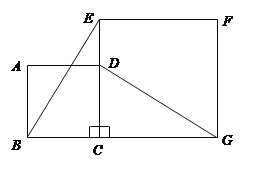
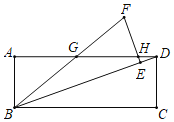
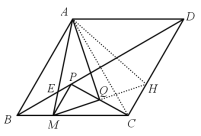
ЁОЬтФПЁПвбжЊСтаЮABCDжаЃЌЁЯABC=60ЁуЃЌAB=4ЃЌЕуMдкBCБпЩЯЃЌЙ§ЕуMзїPMЁЮABНЛЖдНЧЯпBDгкЕуPЃЌСЌНгPCЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБBM=1ЪБЃЌЧѓPCЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЩшAMгыBDНЛгкЕуEЃЌЕБЁЯPCM=45ЁуЪБЃЌЧѓжЄЃК![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШЁPCЕФжаЕуQЃЌСЌНгMQЃЌAQЃЎ
ЂйЧыЬНОПAQКЭMQжЎМфЕФЪ§СПЙиЯЕЃЌВЂаДГіЬНОПЙ§ГЬЃЛ
ЂкЁїAMQЕФУцЛ§газюаЁжЕТ№ЃПШчЙћгаЃЌЧыжБНгаДГіетИізюаЁжЕЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂйAQ=
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂйAQ=![]() MQЃЌМћНтЮіЃЌЂкгаЃЌ
MQЃЌМћНтЮіЃЌЂкгаЃЌ![]()
ЁОНтЮіЁП
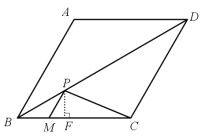
ЃЈ1ЃЉЙ§ЕуPзїPFЁЭBCгкЕуFЃЌЪзЯШРћгУСтаЮЕФаджЪЕУГіЁЯABD=ЁЯCBD=30ЁуЃЌAB=BC=CD=AD=4ЃЌШЛКѓИљОнЦНааЯпЕФаджЪЕУГіЁЯABD=ЁЯBPM=ЁЯCBD=30ЁуЃЌЁЯPMF =ЁЯABC=60ЁуЃЌНјЖјПЩЧѓГіPM,PF,MFЕФГЄЖШЃЌДгЖјFCЕФГЄЖШПЩЧѓЃЌзюКѓРћгУЙДЙЩЖЈРэМДПЩЧѓPCЕФГЄЖШЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPGЁЭBCгкЕуGЃЌЩшMG=xЃЌгЩЃЈ1ЃЉПЩжЊЃКBM=PM=2xЃЌGC=PG=![]() xЃЌШЛКѓРћгУBM+MG+GC=BCЧѓГіxЕФжЕЃЌНјЖјПЩЧѓГіBMЕФГЄЖШЃЌзюКѓРћгУЦНааЯпЗжЯпЖЮГЩБШР§МДПЩЕУГіНсТлЃЛ
xЃЌШЛКѓРћгУBM+MG+GC=BCЧѓГіxЕФжЕЃЌНјЖјПЩЧѓГіBMЕФГЄЖШЃЌзюКѓРћгУЦНааЯпЗжЯпЖЮГЩБШР§МДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЂйбгГЄMQгыCDНЛгкЕуHЃЌСЌНгAH,ACЃЌЪзЯШжЄУїЁїPMQЁеЁїCHQЃЌдђгаPM=CH=BMЃЌMQ=HQЃЌШЛКѓРћгУСтаЮЕФаджЪКЭЕШБпШ§НЧаЮЕФаджЪжЄУї ЁїABMЁеЁїACHЃЌдђгаAM=AHЃЌЁЯBAM=ЁЯCAHЃЌдђЁїAMHЮЊЕШБпШ§НЧаЮЃЌдђРћгУЕШБпШ§НЧаЮЕФаджЪМДПЩЕУГіAQ,MQжЎМфЕФЙиЯЕЃЛ
ЂкИљОнЂйжаЕФНсТлга![]() ЃЌЕБAMШЁзюаЁжЕЪБЃЌMQгазюаЁжЕЃЌЕБ
ЃЌЕБAMШЁзюаЁжЕЪБЃЌMQгазюаЁжЕЃЌЕБ![]() ЪБЃЌAMзюаЁЃЌЧѓГіДЫЪБЕФAM,MQЕФжЕЃЌзюКѓРћгУ
ЪБЃЌAMзюаЁЃЌЧѓГіДЫЪБЕФAM,MQЕФжЕЃЌзюКѓРћгУ![]() ЧѓНтМДПЩЃЎ
ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌЙ§ЕуPзїPFЁЭBCгкЕуFЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌ
ЁрЁЯABD=ЁЯCBD=30ЁуЃЌAB=BC=CD=AD=4ЃЎ
ЁпPMЁЮABЃЌ
ЁрЁЯABD=ЁЯBPM=ЁЯCBD=30ЁуЃЌЁЯPMF =ЁЯABC=60ЁуЃЌ
ЁрPM=BM=1ЃЌ
ЁрMF=![]() PM=
PM=![]() ЃЌPF=
ЃЌPF=![]() ЃЌ
ЃЌ
ЁрFC=BC-BM-MF=4-1-![]() =
=![]() ЃЌ
ЃЌ
ЁрPC=![]() =
=![]() ЃЎ
ЃЎ
ЃЈ2ЃЉжЄУїЃКШчЭМЃЌЙ§ЕуPзїPGЁЭBCгкЕуGЃЎ
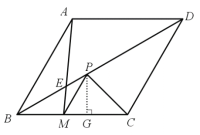
ЁпЁЯPCM=45ЁуЃЌ
ЁрЁЯCPG=ЁЯPCM=45ЁуЃЌ
ЁрPG=GCЃЎ
ЩшMG=xЃЌгЩЃЈ1ЃЉПЩжЊЃКBM=PM=2xЃЌGC=PG=![]() xЃЌ
xЃЌ
гЩBM+MG+GC=BCЕУЃК2x+x+![]() x=4ЃЌ
x=4ЃЌ
Ёрx=![]() ЃЌ
ЃЌ
ЁрBM=![]() ЃЎ
ЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрBMЁЮADЃЌ
Ёр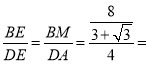
![]()
ЃЈ3ЃЉЂйШчЭМЃЌбгГЄMQгыCDНЛгкЕуHЃЌСЌНгAH,ACЃЎ
ЁпPMЁЮABЁЮCDЃЌ
ЁрЁЯPMQ=ЁЯCHQЃЌЁЯMPQ=ЁЯHCQЃЎ
ЁпQЪЧPCЕФжаЕуЃЌ
ЁрPQ=CQЃЌ
ЁрЁїPMQЁеЁїCHQЃЌ
ЁрPM=CH=BMЃЌMQ=HQЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌ
ЁрЁїABCЮЊЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌЁЯABM=ЁЯACH=60ЁуЃЌ
ЁрЁїABMЁеЁїACHЃЌ
ЁрAM=AHЃЌЁЯBAM=ЁЯCAHЃЌ
ЁрЁЯMAH=ЁЯBAC=60ЁуЃЌ
ЁрЁїAMHЮЊЕШБпШ§НЧаЮЃЌ
ЁрAQЁЭMHЃЌЁЯMAQ=![]() ЁЯMAH=30ЁуЃЌ
ЁЯMAH=30ЁуЃЌ
ЁрAQ=![]() MQЃЎ
MQЃЎ
ЂкЁпAQЁЭMHЃЌЁЯMAQ=![]() ЁЯMAH=30ЁуЃЌ
ЁЯMAH=30ЁуЃЌ
![]() ЃЌ
ЃЌ
ЁрЕБAMШЁзюаЁжЕЪБЃЌMQгазюаЁжЕЃЎ
ЕБ![]() ЪБЃЌAMзюаЁЃЌДЫЪБ
ЪБЃЌAMзюаЁЃЌДЫЪБ![]() ЃЌ
ЃЌ
ЁрMQЕФзюаЁжЕЮЊ![]() ЃЌ
ЃЌ
ДЫЪБ![]()
ЁрЁїAMQЕФУцЛ§газюаЁжЕЃЌзюаЁжЕЮЊ![]()

 Н№ХЦНЬИЈХргХгХбЁОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ
Н№ХЦНЬИЈХргХгХбЁОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ