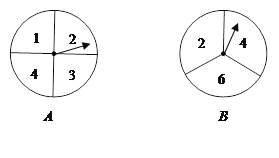
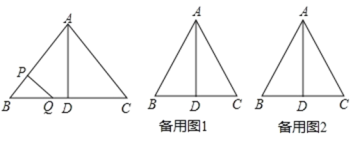
��Ŀ����
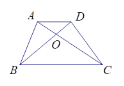
����Ŀ����ͼ������������������A��B��O���㣬����ã�3��3����ʾ����ֽ��A���λ�ã���1��1����ʾB���λ�ã�O��Ҳ��������ϣ�
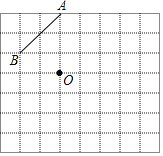
��1��������B����ֱ��OA����ԳƵ�C��д����C���꣮����д��������Ҫ��ͼ�б����ĸ����
��2��������ABC���ڵ�O�����ĶԳ�ͼ�Ρ�A��B��C�䣬д��A�䡢B�䡢C����������ꣻ����д��������Ҫ�����ĸ����
��3���������ϵ���С�����α߳�Ϊ1�������A��B��C��������
���𰸡���1����������C��5��1������2����ͼ��������A'��3����3����B'��5����1����C����1����1������3��4
��������
��1���ȸ������⻭��ֱ������ϵ��Ȼ�������Գ�ͼ�ε���������C�㼴�ɣ�
��2���ɣ�1���õ�����ABC��O��Ϊ������ת180�㼴�ɵý⣻
��3������ͼ�����ֱ꣬�����������ε������ʽ��⼴��.
�⣺��1����ͼ��ʾ����C��Ϊ����C��5��1����.
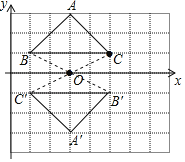
��2����ͼ��ʾ����A��B��C������Ϊ����A'��3����3����B'��5����1����C����1����1����
��3����A��B��C���������S��A'B'C����![]() ��4��2��4��
��4��2��4��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ