ЬтФПФкШн
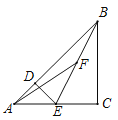
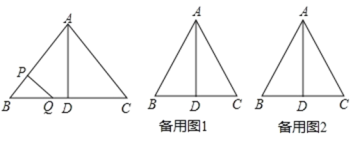
ЁОЬтФПЁПШчЭМ,ЁїABCжа,AB=AC=10РхУз,BC=12РхУз,DЪЧBCЕФжаЕу,ЕуPДгBГіЗЂ,вдaРхУз/Уы(a>0)ЕФЫйЖШбиBAдШЫйЯђЕуAдЫЖЏЃЌЕуQЭЌЪБвд1РхУз/УыЕФЫйЖШДгDГіЗЂЃЌбиDBдШЫйЯђЕуBдЫЖЏЃЌЦфжавЛИіЖЏЕуЕНДяжеЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЌЩшЫќУЧЕФдЫЖЏЪБМфЮЊtУыЁЃ
(1)Шєa=![]() ЃЌt=2,ЧѓжЄЃКЁїABCЁзЁїPBQЃЈ2ЃЉШєa=2ЃЌФЧУДtЮЊКЮжЕЪБЃЌвд BЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABDЯрЫЦ?ЫЕУїРэгЩЁЃ
ЃЌt=2,ЧѓжЄЃКЁїABCЁзЁїPBQЃЈ2ЃЉШєa=2ЃЌФЧУДtЮЊКЮжЕЪБЃЌвд BЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABDЯрЫЦ?ЫЕУїРэгЩЁЃ
ЁОД№АИЁП(1)МћНтЮі;(2)МћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтНЋPBгкBQЕФГЄЗжБ№МЦЫуГіРДЃЌШЛКѓИљОн![]() вдМАЁЯB=ЁЯBжЄУїМДПЩ
вдМАЁЯB=ЁЯBжЄУїМДПЩ
ЃЈ2ЃЉИљОнЬтвтЃЌвЛЙВгаСНжжЯрЫЦЧщПіЃКЁїBPQЁзЁїBDAЛђЁїBQPЁзЁїBDAЃЌШЛКѓРћгУДњЪ§ЪНБэДяГіИїздЧщПіЯТBPЁЂBQЕФжЕЃЌРћгУШ§НЧаЮЯрЫЦЕФаджЪНЈСЂЗНГЬМЦЫуМДПЩ
ЃЈ1ЃЉЕБt=2ЪБЃЌBP=![]() ЃЛBQ=
ЃЛBQ=![]()
Ёр![]() =
=![]()
гжЁпЁЯB=ЁЯB
ЁрЁїABCЁзЁїPBQ
(2)ЕБ![]() ЪБЃЌBP=2tЃЌDQ=t
ЪБЃЌBP=2tЃЌDQ=t
ЁпDЪЧBCжаЕуЃЌBC=12
ЁрBD=DC=6
ЁрBQ=6-t
ЕБЁїBPQЁзЁїBDAЪБЃЌ
дђгаЃК![]()
ЁпBP=2tЃЌBD=6,BQ=6-t,BA=10
Ёр![]()
НтЕУ![]()
ЕБЁїBQPЁзЁїBDAЪБЃЌ
дђга![]()
ЁпBP=2tЃЌBD=6,BQ=6-t,BA=10
Ёр![]()
НтЕУ![]()
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() sЛђ
sЛђ![]() sЪБЃЌЁїBQPгыЁїBDAЯрЫЦ
sЪБЃЌЁїBQPгыЁїBDAЯрЫЦ

 аТПЮБъПьРжЬсгХЪюМйзївЕЩТЮїТУгЮГіАцЩчЯЕСаД№АИ
аТПЮБъПьРжЬсгХЪюМйзївЕЩТЮїТУгЮГіАцЩчЯЕСаД№АИ ЪюМйЯЮНгХргХНЬВФеуНЙЄЩЬДѓбЇГіАцЩчЯЕСаД№АИ
ЪюМйЯЮНгХргХНЬВФеуНЙЄЩЬДѓбЇГіАцЩчЯЕСаД№АИ