题目内容
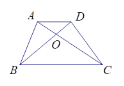
【题目】如图，梯形ABCD中，AD//BC，对角线AC、BD相交于点O ，若
,则
等于（）
A. 1：6B. 1：3C. 1：4D. 1：5
【答案】C
【解析】
由AD与BC平行，利用两直线平行得到两对内错角相等，利用两对角相等的三角形相似得到三角形AOD与三角形BOC相似，由三角形AOD与三角形ACD面积之比求出三角形AOD与三角形COD面积之比，进而得出OA与OC之比，利用相似三角形面积之比等于相似比的平方即可求出所求面积之比．
解：∵AD∥BC，
∴∠DAC=∠ACB，∠ADB=∠DBC，
∴△AOD∽△COB，
∵S△AOD：S△ACD=1：3，
∴S△AOD：S△DOC=1：2，即OA：OC=1：2，
∴S△AOD：S△BOC=1：4，
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
