Question

【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0)，且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】

（1）把点（-1，0）代入解析式可得ab+c=0①，结合4a+2b+c>0②，即可整理出a+b>0；

（2）由②+①×2得，6a+3c>0，结合a<0，故可求出a+c>0；

（3）画草图可知c>0，结合a-b+c=0，可整理得-a+b+c=2c>0，从而求得-a+b+c>0；

（4）由ab+c=0可得，b22ac5a2=(c+2a)(c2a)，由（2）可知2a+c>0，再由a<0， c>0可知c-2a>0，故可得出（c+2a）（c-2a）>0，即b2-2ac-5a2>0，进而可得出结论．

(1) ∵抛物线y=ax2+bx+c(a<0)经过点(1,0)，

∴原式可化为ab+c=0①，

又∵4a+2b+c>0②，

∴②①得：

3a+3b>0，

即a+b>0，

故正确；

(2)②+①×2得，

6a+3c>0，

即2a+c>0，

∴a+c>a，

∵a<0，

∴a>0，

∴a+c>0；

故正确；

(3)因为4a+2b+c>0,可以看作y=ax2+bx+c(a<0)当x=2时的值大于0，草图为：

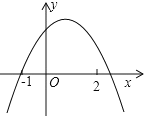
可见c>0,

∵ab+c=0，

∴a+bc=0，

两边同时加2c得a+bc+2c=2c，

整理得a+b+c=2c>0，

即a+b+c>0；

故正确；

(4)∵过(1,0)，代入得ab+c=0，

∴b22ac5a2=(a+c)22ac5a2=c24a2=(c+2a)(c2a)

由（2）可知2a+c>0，

由（3）可知c>0，

∵a<0，

∴c2a>0②

∴(c+2a)(c2a)>0，

∴b22ac5a2>0，

即b22ac>5a2，

故正确.

∴正确的个数有4个.

故选D.