题目内容
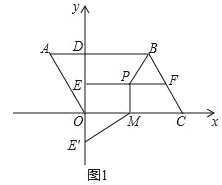
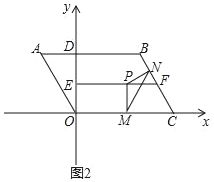
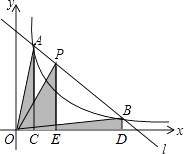
【题目】如图，等腰Rt△ABC中，∠BAC=90°，AB=AC=10，等腰直角三角形ADE绕着点A旋转，∠DAE=90°，AD=AE=6，连接BD、CD、CE，点M、P、N分别为DE、DC、BC的中点，连接MP、PN、MN，则△PMN的面积最大值为_____．
【答案】32
【解析】
由题意可证△ADB≌△EAC，可得BD=CE，∠ABD=∠ACE，由三角形中位线定理可证△MPN是等腰直角三角形，则S△PMN=
PN2=
BD2．可得BD最大时，△PMN的面积最大，由等腰直角三角形ADE绕着点A旋转，可得D是以A为圆心，AD=6为半径的圆上一点，可求BD最大值，即可求△PMN的面积最大值．
∵△ABC，△ADE是等腰直角三角形，
∴AD=AE，AB=AC，∠BAC=∠DAE=90°，
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，
∴∠BAD=∠CAE且AB=AC，AD=AE，
∴△ADB≌△AEC，
∴DB=EC，∠ABD=∠ACE．
∵M，N，P分别是DE，DC，BC的中点，
∴MP∥EC，MP=EC，NP=DB，NP∥BD，
∴MP=NP，∠DPM=∠DCE，∠PNC=∠DBC．
设∠ACE=x°，∠ACD=y°，
∴∠ABD=x°，∠DBC=45°﹣x°=∠PNC，∠DCB=45°﹣y°，
∴∠DPM=x°+y°，∠DPN=∠DCB+∠PNC=∠DCB+∠DBC=45°﹣y°+45°﹣x°=90°﹣x°﹣y°，
∴∠MPN=90°且PN=PM，
∴△PMN是等腰直角三角形，∴S△PMN=PN2=BD2，∴当BD最大时，△PMN的面积最大．
∵D是以A点为圆心，AD=6为半径的圆上一点，
∴A，B，D共线且D在BA的延长线时，BD最大．
此时BD=AB+AD=16，
∴△PMN的面积最大值为32．
故答案为：32．
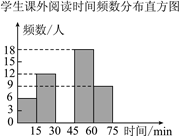
【题目】某校要了解学生每天的课外阅读时间情况，随机调查了部分学生，对学生每天的课外阅读时间x(单位：min)进行分组整理，并绘制了如图所示的不完整的统计图表，根据图中提供的信息，解答下列问题：
(1)本次调查共抽取了________名学生；
(2)统计表中a＝________，b＝________；
(3)将频数分布直方图补充完整；
(4)若全校共有1200名学生，请估计阅读时间不少于45 min的有多少人.
课外阅读时间x/min | 频数/人 | 百分比 |
0≤x＜15 | 6 | 10% |
15≤x＜30 | 12 | 20% |
30≤x＜45 | a | 25% |
45≤x＜60 | 18 | b |
60≤x＜75 | 9 | 15% |
