Question

【题目】如图，直线l和双曲线 （k＞0）交于A，B两点，P是线段AB上的点（不与A，B重合），过点A，B，P分别向x轴作垂线，垂足分别是C，D，E，连接OA，OB，OP，设△AOC面积是S1 ， △BOD面积是S2 ， △POE面积是S3 ， 则（ ）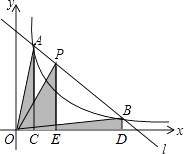
A.S1＜S2＜S3
B.S1＞S2＞S3
C.S1=S2＞S3
D.S1=S2＜S3

Answer 1

【答案】D
【解析】解：如下图，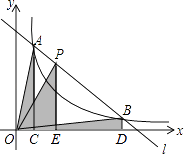
∵点A在y= 上，
∴S△AOC= k，
∵点P在双曲线的上方，
∴S△POE＞ k，
∵点B在y= 上，
∴S△BOD= k，
∴S1=S2＜S3 ．
故选；D．
【考点精析】利用比例系数k的几何意义对题目进行判断即可得到答案，需要熟知几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积．