题目内容
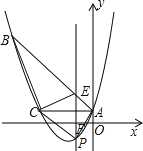
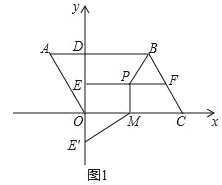
【题目】如图1,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.
(1)请直接写出点A的坐标为_____,点B的坐标为_____;
(2)当BP+PM+ME′的长度最小时,请直接写出此时点P的坐标为_____;
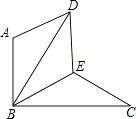
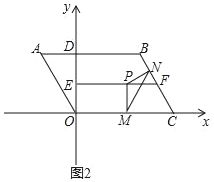
(3)如图2,点N为线段BC上的动点且CM=CN,连接MN,是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的EP的值;若不存在,请说明理由.
【答案】(1)(﹣2,2![]() ),(4,2
),(4,2![]() );(2)(2,
);(2)(2,![]() );(3)EP的值为3或6﹣
);(3)EP的值为3或6﹣![]() 或5.
或5.
【解析】
(1)由30°直角三角形的性质求出OD的长,再由平行四边形的性质求出BD的长即可解决问题;
(2)首先证明四边形OPME′是平行四边形,可得OP=EM,因为PM是定值,推出PB+ME′=OP+PB的值最小时,BP+PM+ME′的长度最小;
(3)分三种情形画出图形分别求解即可解决问题.
(1)如图1中,
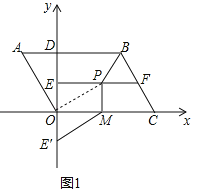
在Rt△ADO中,∵∠A=60°,∴∠AOD=30°.∵AD=2,∴OD =2![]() ,∴A(﹣2,2
,∴A(﹣2,2![]() ),
),
∵四边形ABCO是平行四边形,∴AB=OC=6,∴DB=6﹣2=4,∴B(4,2![]() );
);
(2)如图1中,连接OP.
∵EF垂直平分线段OD,PM⊥OC,∴∠PEO=∠EOM=∠PMO=90°,∴四边形OMPE是矩形,∴PM=OE=![]() .
.
∵OE=OE′,∴PM=OE′,PM∥OE′,∴四边形OPME′是平行四边形,∴OP=EM,
∵PM是定值,∴PB+ME′=OP+PB的值最小时,BP+PM+ME′的长度最小,∴当O、P、B共线时,BP+PM+ME′的长度最小.
∵直线OB的解析式为y=![]() x,∴P(2,
x,∴P(2,![]() ).
).
故答案为:(2,![]() ).
).
(3)如图2中,当PM=PN=![]() 时,
时,
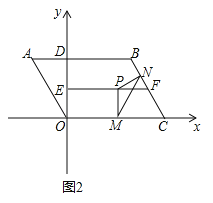
∵AOCB是平行四边形,∴∠MCN=∠A=60°.∵MC=CN,∴△MNC是等边三角形,∴∠CMN=∠CNM=60°.
∵PM⊥OC,∴∠PMN=∠PNM=30°,∴∠PNF=30°+60°=90°,
∵∠PFN=∠BCO=60°,∴∠NPF=30°,NF=1,∴PF=2NF=2,
∵EF=![]() =5,∴PE=5﹣2=3.
=5,∴PE=5﹣2=3.
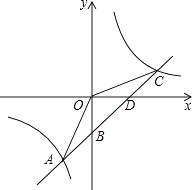
如图3中,当PM=MN时,
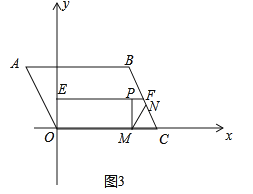
∵PM=MN=CM=![]() ,∴EP=OM=6﹣
,∴EP=OM=6﹣![]() .
.
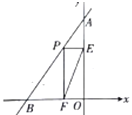
如图4中,当点P与F重合时,NP=NM,此时PE=EF=5.
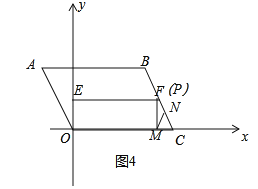
综上所述:满足条件的EP的值为3或6﹣![]() 或5.
或5.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案