Question

【题目】已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.

Answer 1

【答案】y=x+2或y=-x+2

【解析】

试题首先根据题意画出函数图象，分两种情况，但是直线都过（0，2），分别求出A，B点的坐标，再利用待定系数法求出一次函数的解析式．

试题解析：如图：

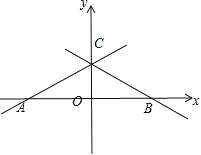
①∵一次函数的图象y=kx+b与两坐标轴围成的三角形的面积是2，

∴OB×CO=2，

×OB×2=2，

BO=2，

∴B（2，0）

∵y=kx+b的图象过点（0，2），（2，0），

∴，

解得：，

∴此一次函数的解析式为：y=-x+2；

②∵一次函数的图象y=kx+b与两坐标轴围成的三角形的面积是2，

∴OA×CO=2，

×OA×2=2，

AO=2，

∴A（-2，0）

∵y=kx+b的图象过点（0，2），（-2，0），

∴，

解得：，

∴此一次函数的解析式为：y=x+2，

综上：此一次函数的解析式为：y=-x+2或y=x+2．