��Ŀ����
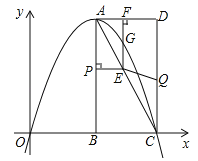
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������![]() ��
��![]() ��
��![]() ������
������![]() ��A��C���㣮
��A��C���㣮
![]() ֱ��д����A�����꣬����������ߵĽ���ʽ��
ֱ��д����A�����꣬����������ߵĽ���ʽ��
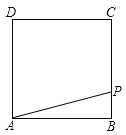
![]() ����P�ӵ�A����
����P�ӵ�A����![]() ���߶�AB���յ�B�˶���ͬʱ��Q�ӵ�C���������߶�CD���յ�D�˶�
���߶�AB���յ�B�˶���ͬʱ��Q�ӵ�C���������߶�CD���յ�D�˶�![]() �ٶȾ�Ϊÿ��1����λ���ȣ��˶�ʱ��Ϊt��
�ٶȾ�Ϊÿ��1����λ���ȣ��˶�ʱ��Ϊt��![]() ����P��
����P��![]() ��AC�ڵ�E��
��AC�ڵ�E��
![]() ����E��
����E��![]() �ڵ�F�����������ڵ�
�ڵ�F�����������ڵ�![]() ��tΪ��ֵʱ���߶�EG���
��tΪ��ֵʱ���߶�EG���
![]() ����
����![]() �ڵ�P��Q�˶��Ĺ����У��ж��м���ʱ��ʹ��
�ڵ�P��Q�˶��Ĺ����У��ж��м���ʱ��ʹ��![]() �ǵ��������Σ���ֱ��д����Ӧ��tֵ��
�ǵ��������Σ���ֱ��д����Ӧ��tֵ��

���𰸡�![]() A������Ϊ
A������Ϊ![]() �������ߵĽ���ʽΪ��
�������ߵĽ���ʽΪ��![]() ��
��![]() ��
��![]() ʱ���߶�EG�Ϊ2��
ʱ���߶�EG�Ϊ2��![]() ��
��
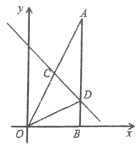
����������������1�������ı���ABCDΪ����������A����D����������ͬ��A����B���������ͬ��
��2���ٸ������������ε����������E�ĺ��������ʽ��Ϊ��G�ĺ��������ʽ��������κ�������ʽ������ݱ����ʽ�����߶���ֵ����ת��Ϊ���κ�����ֵ������
�������ɵ�������������������������������ȼ��������ǿɷ�EQ=QC��EC=CQ��EQ=EC����������ۣ������������ʱ����ͬ�������߳�����ͬ��Ϊ���������Σ�
�������1����Ϊ��B�ĺ�����Ϊ4����D��������Ϊ8��AD��x����AB��y�������Ե�A������Ϊ��4��8����
��A��4��8����C��8��0����������ֱ����y=ax2+bx��![]() �������a=��
�������a=��![]() ��b=4�� �������ߵĽ���ʽΪ��y=��
��b=4�� �������ߵĽ���ʽΪ��y=��![]() x2+4x��
x2+4x��
��2������Rt��APE��Rt��ABC����tan��PAE=![]() =
=![]() ����
����![]() =
=![]() ����PE=
����PE=![]() AP=
AP=![]() t��PB=8��t�����E��������4+
t��PB=8��t�����E��������4+![]() t��8��t�������G������������
t��8��t�������G������������![]() ��4+
��4+![]() t��2+4��4+
t��2+4��4+![]() t��=��
t��=��![]() t2+8����EG=��
t2+8����EG=��![]() t2+8����8��t��=��
t2+8����8��t��=��![]() t2+t��
t2+t��
����![]() ��0���൱t=4ʱ���߶�EG�Ϊ2��
��0���൱t=4ʱ���߶�EG�Ϊ2��
�ڹ�������ʱ�̣�
��i����EQ=QCʱ����ΪQ��8��t����E��4+![]() t��8��t����QC=t�����Ը����������빫ʽ��������
t��8��t����QC=t�����Ը����������빫ʽ��������![]() t��4��2+��8��2t��2=t2��
t��4��2+��8��2t��2=t2��
��������13t2��144t+320=0�������t=![]() ��t=
��t=![]() =8����ʱE��C�غ������ܹ�������������ȥ����
=8����ʱE��C�غ������ܹ�������������ȥ����
��ii����EC=CQʱ����ΪE��4+![]() t��8��t����C��8��0����QC=t�����Ը����������빫ʽ������
t��8��t����C��8��0����QC=t�����Ը����������빫ʽ������
��4+![]() t��8��2+��8��t��2=t2��
t��8��2+��8��t��2=t2��
��������t2��80t+320=0��t=40��16![]() ��t=40+16
��t=40+16![]() ��8����ʱQ���ھ��εı�������ȥ����
��8����ʱQ���ھ��εı�������ȥ����
��iii����EQ=ECʱ����ΪQ��8��t����E��4+![]() t��8��t����C��8��0�������Ը����������빫ʽ��������
t��8��t����C��8��0�������Ը����������빫ʽ��������![]() t��4��2+��8��2t��2=��4+/span>
t��4��2+��8��2t��2=��4+/span>![]() t��8��2+��8��t��2�������t=0����ʱQ��C�غ������ܹ�������������ȥ����t=
t��8��2+��8��t��2�������t=0����ʱQ��C�غ������ܹ�������������ȥ����t=![]() ��
��
����t1=![]() ��t2=
��t2=![]() ��t3=40��16
��t3=40��16![]() ��
��

����Ŀ����ͼ�����������Ƕ���ʯ�ݣ���ͼ�ֱ��ʾ�ݵ�һ��������ʱ���������ô����������ȥ
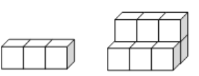
һ�� ����
������±���δ������գ��۲���ɡ�
���ݼ��� | һ�� | ���� | ���� | �ļ� |
ʯ�տ��� | 3 | 9 |
�ڵ���n������ʱ������������ʯ��_______________�飨��n�Ĵ���ʽ��ʾ��