题目内容
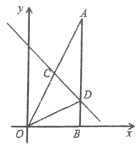
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
【答案】(1)y=2x; (2)![]() ;(3)点M的坐标为(
;(3)点M的坐标为(![]() ,0).
,0).
【解析】
(1)先求出点A的坐标,然后设直线AO的解析式为y=kx,用待定系数法求解即可;
(2)由面积法求出BD的长,从而求出点D的坐标,然后带入y=-x+b求解即可;
(3)先求出点C的坐标,作点C关于x轴的对称点E,此时M到A、C的距离之和最小,求出直线AE的解析式,即可求出点M的坐标.
(1)![]() OB=4,AB=8,∠ABO=90°,
OB=4,AB=8,∠ABO=90°,
∴A点坐标为(4,8),
设直线AO的解析式为y=kx,则4k=8 ,
解得k=2,即直线AO的解析式为y=2x;
(2)![]() OB=4,∠ABO=90°,
OB=4,∠ABO=90°,![]() =4,
=4,
∴DB=2,∴D点的坐标为(4,2),
把D(4,2)代入![]() 得:
得:![]() =6,
=6,
∴直线CD的解析式为![]() ;
;
(3)由直线![]() 与直线
与直线![]() 组成方程组为
组成方程组为![]() ,
,
解得:![]() ,
,
∴点C的坐标为(2,4)
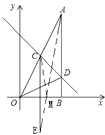
如图,设点M使得MC+MA最小,作点C关于x轴的对称点E,可得点E的坐标为(2,-4),连结MC、ME、AE,可知MC=ME,所以M到A、C的距离之和MA+MC=MA+ME,又MA+ME大于等于AE,所以当MA+ME=AE时,M到A、C的距离之和最小,此时A、M、E成一条直线,M点是直线AE与在x轴的交点.
所以设直线AE的解析式为![]() ,把A(4,8)和E(2,-4)代入
,把A(4,8)和E(2,-4)代入![]() 得:
得:
![]() ,
,
解得:![]() ,
,
所以直线AE的解析式为![]() ,令
,令![]() 得
得![]() ,
,
所以点M的坐标为(![]() ,0).
,0).

练习册系列答案
相关题目