Question

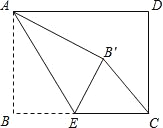
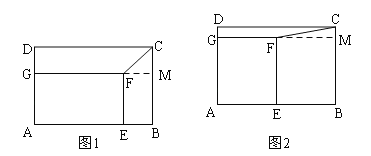
【题目】如图，在矩形ABCD中，AB=12，BC=9，点E，G分别为边AB，AD上的点，若矩形AEFG与矩形ABCD相似，且相似比为，连接CF，则CF=　 　．

Answer 1

【答案】5或．

【解析】分析：若矩形AEFG与矩形ABCD相似，没确定哪两条边相似，所以分两种情况：

①当AD与AG对应时，先根据相似比求AG和AE的长，利用线段的差求FM和CM的长，根据勾股定理求CF的长；

②当AD与AE对应时，同理可得CF的长．

详解：延长GF交BC于M．∵四边形AEFG和ABCD是矩形，∴GF∥AE．∵AB⊥BC，∴GM⊥BC，分两种情况：

①当AD与AG对应时．∵相似比为．∵AB=12，AD=BC=9，∴EF=AG=BM=6，GF=AE=8，∴FM=12﹣8=4，CM=9﹣6=3．在Rt△CMF中，由勾股定理得：CF==5。

②当AD与AE对应时．∵相似比为，∴AG=8，AE=6，∴FM=12﹣6=6，CM=9﹣8=1．在Rt△CMF中，由勾股定理得：CF==．

故答案为：5或．